题目内容
锐角△ABC的三边长度分别是a-1，a，a+1，则a的取值范围是 ．
考点：余弦定理
专题：解三角形
分析：判断得到a+1为最大边，设它对的角为α，利用余弦定理表示出cosα，根据cosα大于0求出a的范围即可．
解答：
解：∵锐角△ABC的三边长度分别是a-1，a，a+1，且最大边a+1对的角为α，
∴cosα=
＞0，即
=
＞0，
解得：a＞4或a＜1，
∵a-1＞0，a＞0，a+1＞0，
∴a＞1，即a＜1不合题意，舍去，
则a的范围为（4，+∞）．
故答案为：（4，+∞）
∴cosα=
| (a-1)2+a2-(a+1)2 |
| 2a(a-1) |
| a(a-4) |
| 2a(a-1) |
| a-4 |
| 2(a-1) |
解得：a＞4或a＜1，
∵a-1＞0，a＞0，a+1＞0，
∴a＞1，即a＜1不合题意，舍去，
则a的范围为（4，+∞）．
故答案为：（4，+∞）
点评：此题考查了余弦定理，以及余弦函数的性质，熟练掌握余弦定理是解本题的关键．
练习册系列答案
相关题目
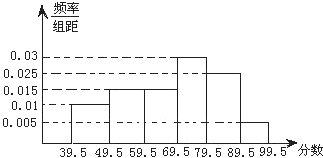如图，从参加环保知识竞赛的学生中抽出60名，将其成绩（均为整数）整理后画出的频率分布直方图如图：观察图形，回答下列问题：若f（sin x）=3-cos 2x，则f（cos x）=（ ）
| A、3-cos 2x |
| B、3-sin 2x |
| C、3+cos 2x |
| D、3+sin 2x |