题目内容
已知{an}是首项为1的等比数列,Sn是{an}的前n项和,且9S3=S6,则通项an为 .
考点:等比数列的性质
专题:计算题,等差数列与等比数列
分析:因为数列an是首项为1的等比数列,且S6=9S3所以公比一定不是1,设公比为q,利用S6=9S3建立公比q的方程求解出公比即可.
解答:
解:因为数列an是首项为1的等比数列,且S6=9S3,
设公比为q,则q≠1,
∵9S3=S6,
∴
=
∴q=2;
所以数列an的通项公式为:an=2n-1
故答案为:an=2n-1.
设公比为q,则q≠1,
∵9S3=S6,
∴
| 9(1-q3) |
| 1-q |
| 1-q6 |
| 1-q |
∴q=2;
所以数列an的通项公式为:an=2n-1
故答案为:an=2n-1.
点评:此题考查了等比数列的前n项和公式及等比数列的通项公式及一元高次方程因式分解求值.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
已知集合M={-1,0,1},N={0,1,2},则M∩N=( )
| A、{-1,0,1} |
| B、{-1,0,1,2} |
| C、{-1,0,2} |
| D、{0,1} |
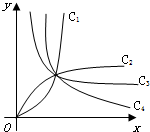 如图的曲线是幂函数y=xn在第一象限内的图象,已知n分别取a,b,c,d四个值,与曲线C1,C2,C3,C4相应,则a,b,c,d四个值从小到大依次为
如图的曲线是幂函数y=xn在第一象限内的图象,已知n分别取a,b,c,d四个值,与曲线C1,C2,C3,C4相应,则a,b,c,d四个值从小到大依次为 根据下面的要求,求满足1+2+3+…+n>500的最小的自然数n.
根据下面的要求,求满足1+2+3+…+n>500的最小的自然数n.