题目内容
命题p:“?x∈[0,+∞),2x-a≥0”,命题q:“?x0∈R,x02+2ax0+2-a=0”,若“p且q”为假命题,求实数a的取值范围.
考点:复合命题的真假
专题:简易逻辑
分析:先根据指数函数的单调性,一元二次方程有实根时判别式△的取值情况即可求出命题p,q下a的取值范围,而由“p且q”为假知p假或q假,所以求p假,q假时a的取值范围再求并集即可.
解答:
解:若p是真命题.则a≤2x对?x∈[0,+∞)恒成立;
则2x的最小值为1,∴a≤1;
若q为真命题,则方程x2+2ax+2-a=0有实根;
∴△=4a2-4(2-a)≥0,即a≥1或a≤-2;
若“p且q”为假命题,则p假,或q假;
∴a>1,或-2<a<1;
∴实数a的取值范围为(-2,1)∪(1,+∞).
则2x的最小值为1,∴a≤1;
若q为真命题,则方程x2+2ax+2-a=0有实根;
∴△=4a2-4(2-a)≥0,即a≥1或a≤-2;
若“p且q”为假命题,则p假,或q假;
∴a>1,或-2<a<1;
∴实数a的取值范围为(-2,1)∪(1,+∞).
点评:考查指数函数的单调性,含参数的式子恒成立时的解决方法,一元二次方程有实根时判别式△的取值情况,以及p且q的真假和p,q真假的关系.

练习册系列答案
相关题目
下列函数中,定义域是R+且为增函数的是( )
| A、y=e-x |
| B、y=x |
| C、y=lnx |
| D、y=|x| |
设f(x)为定义在R上的奇函数,当x≥0时,f(x)=3x-2x+b(b为常数),则f(-1)=( )
A、
| ||
| B、1 | ||
| C、-1 | ||
| D、0 |
已知集合A={-1,0},B={0,1},则集合∁A∪B(A∩B)( )
| A、φ | B、{0} |
| C、{-1,1} | D、{-1,0,1} |
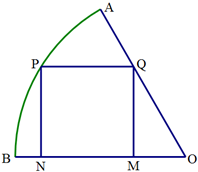 如图,在半径为
如图,在半径为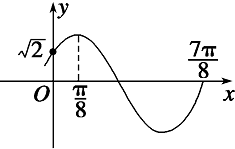 函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<
函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<