题目内容
若对?x∈[-1,1],不等式x2+mx+3m>0恒成立,求实数m的取值范围.
考点:函数恒成立问题
专题:函数的性质及应用
分析:通过y=x2+mx+3m,判断开口方向,求出函数的对称轴,利用二次函数的最值求解即可.
解答:
解:∵y=x2+mx+3m,x∈[-1,1],y>0恒成立.函数的对称轴为x=-
,开口向上,
①当-
<-1,即m>2时,只需f(-1)>0即可,
可得
,解得m>2.
②当-
>1,即m<-2时,只需f(1)>0即可,
可得
,解得m∈∅.
③当-1≤-
≤1,即-2≤m≤2时,只需f(-
)>0即可,
可得
,解得0<m≤2.
综上实数m的取值范围:(0,+∞).
| m |
| 2 |
①当-
| m |
| 2 |
可得
|
②当-
| m |
| 2 |
可得
|
③当-1≤-
| m |
| 2 |
| m |
| 2 |
可得
|
综上实数m的取值范围:(0,+∞).
点评:本题主要考查了函数恒成立问题的求解,分类讨论以及转化思想的应用,二次函数闭区间是的最值以及单调性的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
空间两条异面直线是指它们( )
| A、没有公共点 |
| B、不在同一平面内 |
| C、分别在两个不同的平面内 |
| D、不同在任何一个平面内 |
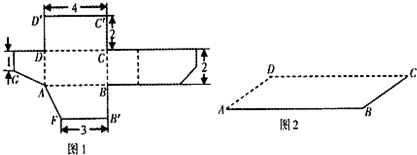 某长方体截去一个三棱锥后,形成的几何体的平面展开图的一部分如图1所示.
某长方体截去一个三棱锥后,形成的几何体的平面展开图的一部分如图1所示.