题目内容
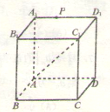 如图,P是正方体ABCD-A1B1C1D1棱A1D1上一点,设点P和直线AC1确定的平面为α,过点P与直线AC1垂直的平面为β,则下列命题正确的是
如图,P是正方体ABCD-A1B1C1D1棱A1D1上一点,设点P和直线AC1确定的平面为α,过点P与直线AC1垂直的平面为β,则下列命题正确的是①存在平面α,使得A1B∥α;
②对任意平面α都有α⊥β;
③平面α将正方体分割为体积相等的两部分;
④β截正方体所得截面多边形可能是四边形.
考点:命题的真假判断与应用
专题:空间位置关系与距离
分析:可取P为A1D1的中点,运用线面平行的判定定理,即可判断①;由面面垂直的判定定理可判断②;运用正方体的对称性即可判断③;可根据截面A1BD和截面B1CD1都和直线AC1垂直,可知β截正方体所得截面介于截面A1BD和截面B1CD1之间,从而判断④.
解答:
解:①当P为A1D1的中点时,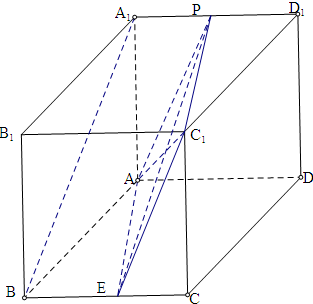
取BC的中点E,连C1E,可证PA∥C1E,
连PE,可得A1B∥PE,
由线面平行的判定定理可得A1B∥α,故①正确;
②因为平面α过AC1,且AC1⊥β,所以α⊥β,
故②正确;
③由于平面α经过直线AC1,
由对称性易知③正确;
④由于AC1⊥截面A1BD和AC1⊥截面B1CD1,
β截正方体所得截面介于截面A1BD和截面B1CD1之间,可以是三角形或六边形,故④错.
故答案为:①②③

取BC的中点E,连C1E,可证PA∥C1E,
连PE,可得A1B∥PE,
由线面平行的判定定理可得A1B∥α,故①正确;
②因为平面α过AC1,且AC1⊥β,所以α⊥β,
故②正确;
③由于平面α经过直线AC1,
由对称性易知③正确;
④由于AC1⊥截面A1BD和AC1⊥截面B1CD1,
β截正方体所得截面介于截面A1BD和截面B1CD1之间,可以是三角形或六边形,故④错.
故答案为:①②③
点评:本题主要考查空间直线与平面的位置关系,考查线面平行的判断和线面垂直、面面垂直的判定,同时考查空间想象能力和判断能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
复数(3+2i)i等于( )
| A、-2-3i | B、-2+3i |
| C、2-3i | D、2+3i |
设θ为两个非零向量
,
的夹角,已知对任意实数t,|
+t
|的最小值为1.( )
| a |
| b |
| b |
| a |
A、若θ确定,则|
| ||
B、若θ确定,则|
| ||
C、若|
| ||
D、若|
|
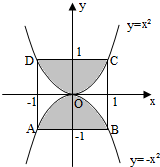 正方形的四个顶点A(-1,-1),B(1,-1),C(1,1),D(-1,1)分别在抛物线y=-x2和y=x2上,如图所示,若将一个质点随机投入正方形ABCD中,则质点落在图中阴影区域的概率是
正方形的四个顶点A(-1,-1),B(1,-1),C(1,1),D(-1,1)分别在抛物线y=-x2和y=x2上,如图所示,若将一个质点随机投入正方形ABCD中,则质点落在图中阴影区域的概率是