题目内容
19.设数列{an}的前n项和为Sn,且a1=1,an+1=3Sn(n∈N*).(1)求数列{an}的通项公式;
(2)设bn=n•an,求数列{bn}的前n项的和.
分析 (1)利用递推关系、等比数列的通项公式即可得出;
(2)设bn=n•an=$\left\{\begin{array}{l}{1,n=1}\\{3n•{4}^{n-2},n≥2}\end{array}\right.$,再利用“错位相减法”、等比数列的前n项和公式即可得出.
解答 解:(1)∵a1=1,an+1=3Sn(n∈N*).
∴a2=3a1=3,
当n≥2时,an=3Sn-1,可得:an+1-an=3an,化为an+1=4an,
∴数列{an}从第二项开始是等比数列,公比为4.
∴an=3×4n-2.
∴an=$\left\{\begin{array}{l}{1,n=1}\\{3×{4}^{n-2},n≥2}\end{array}\right.$.
(2)设bn=n•an=$\left\{\begin{array}{l}{1,n=1}\\{3n•{4}^{n-2},n≥2}\end{array}\right.$
∴n≥2时,数列{bn}的前n项的和Tn=1+3(2+3×4+4×42+…+n•4n-2).
4Tn=4+3[2×4+3×42+…+(n-1)×4n-2+n•4n-1],
∴-3Tn=-3+3(2+4+42+…+4n-2-n•4n-1),
∴Tn=1-$(1+\frac{{4}^{n-1}-1}{4-1}-n•{4}^{n-1})$=$\frac{(3n-1)•{4}^{n-1}+1}{3}$.
点评 本题考查了递推关系、“错位相减法”、等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
9.设集合A={x|x2-3x>0},B={x||x|<2},则A∩B=( )
| A. | (-2,0) | B. | (-2,3) | C. | (0,2) | D. | (2,3) |
4.命题“若x≥1,则3x-2x≥1”的逆否命题是( )
| A. | 若3x-2x≥1,则x≥1 | B. | 若3x-2x<1,则x<1 | C. | 若x<1,则3x-2x<1 | D. | 若3x-2x<1,则x≥1 |
11.设f(x)=(2x-1)ex,则f′(0)等于( )
| A. | 1 | B. | -1 | C. | 4 | D. | -4 |
1.双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的右焦点到它的渐进线的距离为( )
| A. | 12 | B. | 4 | C. | 2$\sqrt{3}$ | D. | 2 |
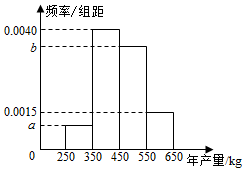 某人租用一块土地种植一种瓜类作物,根据以往的年产量数据,得到年产量频率分布直方图如图所示,以各区间中点值作为该区间的年产量,得到平均年产量为455kg.已知当年产量低于450kg时,单位售价为12元/kg,当年产量不低于450kg 时,单位售价为10元/kg.
某人租用一块土地种植一种瓜类作物,根据以往的年产量数据,得到年产量频率分布直方图如图所示,以各区间中点值作为该区间的年产量,得到平均年产量为455kg.已知当年产量低于450kg时,单位售价为12元/kg,当年产量不低于450kg 时,单位售价为10元/kg.