题目内容
若不等式(a-a2)•(x2+1)+x≤0对一切x∈[(0,2]恒成立,则a的取值范围为( )
A、(-∞,
| ||||||||
B、[
| ||||||||
C、[
| ||||||||
D、(-∞,
|
考点:函数恒成立问题
专题:函数的性质及应用
分析:先将原不等式中的参数分离出来,然后研究不等号右边函数的最值即可,注意基本不等式的应用.
解答:
解:由题意,要使原式成立,只需a-a2≤-
,x∈(0,2]恒成立.
令f(x)=-
=-
,x∈(0,2].
由x∈(0,2]得x+
≥2
=2,当且仅当x=
,即x=1时取等号,
所以-
≥-
,
所以要使原不等式恒成立,只需a-a2≤-
即可,
解得x≤
或x≥
.
故选D.
| x |
| x2+1 |
令f(x)=-
| x |
| x2+1 |
| 1 | ||
x+
|
由x∈(0,2]得x+
| 1 |
| x |
x•
|
| 1 |
| x |
所以-
| 1 | ||
x+
|
| 1 |
| 2 |
所以要使原不等式恒成立,只需a-a2≤-
| 1 |
| 2 |
解得x≤
1-
| ||
| 2 |
1+
| ||
| 2 |
故选D.
点评:本题考查了不等式恒成立问题的解题方法,一般转化为函数的最值问题求解,求参数范围的问题,能分离参数的尽量分离参数.

练习册系列答案
相关题目
点P为底边长为2
,高为2的正三棱柱表面上的动点,MN是该棱柱内切球的一条直径,则
•
取值范围是( )
| 3 |
| PM |
| PN |
| A、[0,2] |
| B、[0,3] |
| C、[0,4] |
| D、[-2,2] |
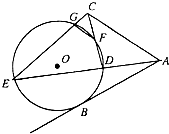 如图,AB是⊙O的一条切线,切点为B,直线ADE,CFD,CGE都是⊙O的割线,已知AC=AB.
如图,AB是⊙O的一条切线,切点为B,直线ADE,CFD,CGE都是⊙O的割线,已知AC=AB. 在长方体ABCD-A1B1C1D1中,AA1=1,AD=DC=
在长方体ABCD-A1B1C1D1中,AA1=1,AD=DC=