题目内容
f(x)=|x3+a|(a∈R)在[-1,1]的最大值为M(a),若g(x)=M(x)-|x2+t|有4个零点,求t的范围.
考点:函数的零点与方程根的关系
专题:综合题,函数的性质及应用
分析:根据条件求出函数M(a)的表达式,然后由g(x)=0得M(x)=|x2+t|,利用函数g(x)=M(x)-|x2+t|有4个零点,建立条件关系即可求出t的取值范围.
解答:
解:当a=0时,f(x)=|x3+a|=|x3|为偶函数,此时最大值为M(a)=M(-1)=M(1),
当a>0时,函数在[-1,1]上的最大值为M(a)=f(1)=|1+a|=a+1,
当a<0时,函数在[-1,1]上的最大值为M(a)=f(-1)=|-1+a|=1-a,
即M(a)=
.
∴M(x)=
.
由g(x)=M(x)-|x2+t|=0得M(x)=|x2+t|,
设函数M(x),m(x)=|x2+t|,
作出两个函数的图象如图:
①若t≤0,要使g(x)=M(x)-|x2+t|有4个零点,
则两个图象的交点个数有4个,此时满足m(0)>M(0),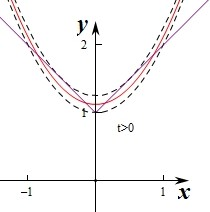
即|t|>1,解得t<-1.
②若t>0,则m(x)=|x2+t|=x2+t,
当抛物线过点(0,1)时,t=1.
当抛物线与直线相切时,当x>0时,
由
,此时x2-x+(t-1)=0,
由判别式△=1-4(t-1)=5-4t=0,
解得t=
.
要使g(x)=M(x)-|x2+t|有4个零点,
则两个图象的交点个数有4个,此时满足1<t<
.
综上t<-1或1<t<
.
当a>0时,函数在[-1,1]上的最大值为M(a)=f(1)=|1+a|=a+1,
当a<0时,函数在[-1,1]上的最大值为M(a)=f(-1)=|-1+a|=1-a,
即M(a)=
|
∴M(x)=
|
由g(x)=M(x)-|x2+t|=0得M(x)=|x2+t|,
设函数M(x),m(x)=|x2+t|,
作出两个函数的图象如图:
①若t≤0,要使g(x)=M(x)-|x2+t|有4个零点,
则两个图象的交点个数有4个,此时满足m(0)>M(0),

即|t|>1,解得t<-1.
②若t>0,则m(x)=|x2+t|=x2+t,
当抛物线过点(0,1)时,t=1.
当抛物线与直线相切时,当x>0时,
由
|
由判别式△=1-4(t-1)=5-4t=0,
解得t=
| 5 |
| 4 |
要使g(x)=M(x)-|x2+t|有4个零点,
则两个图象的交点个数有4个,此时满足1<t<
| 5 |
| 4 |
综上t<-1或1<t<
| 5 |
| 4 |
点评:本题主要考查函数零点个数的应用,利用数形结合是解决本题的关键,根据条件求出M(a)的表达式是本题的难点.注意对t要进行分类讨论.综合性较强,难点大.

练习册系列答案
相关题目
S=1!+2!+3!+…+99!,则S的个位数字为( )
| A、0 | B、3 | C、5 | D、7 |
已知数列 {an} 是等比数列,则下列数列中也一定为等比数列的是( )
| A、{an+1-an} |
| B、{an2} |
| C、{2 an} |
| D、{ln|an|} |
已知函数f(x)=In(2x+
+a)的值域为R,则实数a的取值范围是( )
| 4 |
| 2x |
| A、(-∞,-4) |
| B、(-∞,-4] |
| C、(-4,+∞) |
| D、[-4,+∞) |