题目内容

lim
x→1
xx-1
xlnx
=
 
．
考点：极限及其运算
专题：导数的综合应用
分析：利用导数的运算法则可得：（xx）′=（exlnx）′=xxlnx，（xlnx）′=lnx+1，再利用“罗比达法则”即可得出．
解答： 解：∵（xx）′=（exlnx）′=xxlnx，（xlnx）′=lnx+1，
∴
lim
x→1
xx-1
xlnx
=
lim
x→1
xxlnx
lnx+1
=0，
故答案为：0．
点评：本题考查了导数的运算法则、“罗比达法则”，属于基础题．
练习册系列答案
相关题目
f（x）=|x3+a|（a∈R）在[-1，1]的最大值为M（a），若g（x）=M（x）-|x2+t|有4个零点，求t的范围．
已知△ABC的内角A，B，C所对边分别为a，b，c，且acosC+
1
2
c=b．
（1）求角A的大小；
（2）若bc=2，求边长a的最小值．
（1+x）（1-x）10 展开式中x3的系数为
 
．
设变最x，y满足约束条件 
x+y-2≥0
x-y-2≤0
y≥1
，则目标函数z=x+2（y-l）的最小值为（　　）
A、0B、1C、2D、3
已知角α的终边经过点P（-5，12），则cosα=（　　）
A、
5
13
B、-
5
13
C、
12
13
D、-
12
13
要得到y=cos2x的图象只需将y=cos（-2x+
π
3
）的图象（　　）
A、向左平移
π
3
个单位
B、向左平移
π
6
个单位
C、向右平移
π
6
个单位
D、向右平移
π
3
个单位
在△ABC中，内角A、B、C所对的边分别为a，b，c，已知tanB=
1
2
，tanC=
1
3
，且c=1．
（Ⅰ）求tanA；
（Ⅱ）求a值．
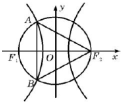如图，F1、F2分别是双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的两个焦点，以坐标原点O为圆心，|OF1|为半径的圆与该双曲线左支交于A、B两点，若△F2AB是等边三角形，则双曲线的离心率为 （　　）
A、
3
B、2
C、
3
-1
D、1+
3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网