题目内容

下列函数中，最小正周期为π的函数是（　　）
A、f（x）=2sin2xcos2x
B、g（x）=
1+tanx
1-tanx
C、h（x）=
2tanx
1-tan2x
D、m（x）=cos2
x
2
-sin2
x
2
考点：三角函数的周期性及其求法
专题：三角函数的图像与性质
分析：利用二倍角公式化简函数的解析式，再利用三角函数的周期性求得它们的周期，从而得出结论．
解答： 解：f（x）=2sin2xcos2x=sin4x的周期为
2π
4
=
π
2
，显然不满足条件；
g（x）=
1+tanx
1-tanx
=tan（x+
π
4
）的周期为π，满足条件；
h（x）=
2tanx
1-tan2x
=tan2x的周期为
π
2
，显然不满足条件；
m（x）=cos2
x
2
-sin2
x
2
=cosx，它的周期为2π，显然不满足条件，
故选：B．
点评：本题主要考查三角函数的周期性，二倍角公式的应用，属于基础题．
练习册系列答案
相关题目
(-1+i)(2+i)
i3
=
 
．
函数f（x）=sinx+cosx，在各项均为正数的数列{an}中对任意的n∈N*都有f（an+x）=f（an-x）成立，则数列{an}的通项公式可以为（写一个你认为正确的）
 
．
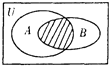
设全集U=R，A={x|x（x+2）＜0，B={x|x＜-1}，则图中阴影部分表示的集合为（　　）
A、{x|-2＜x＜0}
B、{x|-2＜x＜-1}
C、{x|x＞0}
D、{x|x＜-1}
若sinαtanα＞0，且sinαcosα＜0，则α是（　　）
A、第一象限角
B、第二象限角
C、第三象限角
D、第四象限角
若α，β是两个不同平面，m，n是两条不同直线，则下列命题中不正确的是（　　）
A、α∥β，m⊥α，则m⊥β
B、m∥n，m⊥α，则n⊥α
C、n∥α，n⊥β，则α⊥β
D、α∩β=m，n与α，β所成的角相等，则m⊥n
cos（α-35°）cos（α+25°）+sin（α-35°）sin（α+25°）等于（　　）
A、
1
2
B、-
1
2
C、
3
2
D、-
3
2
非零向量
a
，
b
满足|
a
|=|
b
|=|
a
+
b
|，则
a
与
b
的夹角为（　　）
A、
π
3
B、
2π
3
C、
π
6
D、
5π
6
若方程x3+ax2+bx+c=0有三个不等实根x1，x2，x3则x1+x2+x3等于（　　）
A、-aB、-bC、cD、b

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网