题目内容
平面直角坐标系xoy中,直线x-y+1=0截以原点O为圆心的圆所得的弦长为
.
(1)求圆O的方程;
(2)过点P(
,2)的直线l与圆O相切,求直线l的方程.
| 6 |
(1)求圆O的方程;
(2)过点P(
| 2 |
考点:直线与圆的位置关系
专题:直线与圆
分析:(1)画出图形,结合图形,利用勾股定理求出圆O的半径,写出圆O的标准方程;
(2)讨论直线l的斜率是否垂直,利用圆心O到直线l的距离d=r,求出斜率,得出直线l的方程.
(2)讨论直线l的斜率是否垂直,利用圆心O到直线l的距离d=r,求出斜率,得出直线l的方程.
解答:
解:(1)画出图形,如图所示;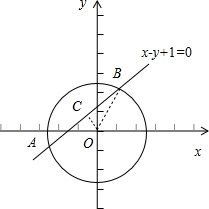
过点O作OC垂直于直线AB,垂足为C,连接OB,
OC=
=
,
∴圆O的半径为OB=
=
=
;
∴圆O的标准方程为x2+y2=2;
(2)设直线l的斜率为k,则直线过点P(
,2),
方程为y-2=k(x-
),
即kx-y+2-
k=0;
又圆心O到直线l的距离为d=r,
∴
=
,
解得k=
,
此时圆的切线方程为
x-4y+6=0;
当斜率k不存在时,圆的切线方程为x-
=0;
综上,切线l的方程为
x-4y+6=0或x-
=0.

过点O作OC垂直于直线AB,垂足为C,连接OB,
OC=
| |1×0-1×0+1| | ||
|
| ||
| 2 |
∴圆O的半径为OB=
OC2+(
|
(
|
| 2 |
∴圆O的标准方程为x2+y2=2;
(2)设直线l的斜率为k,则直线过点P(
| 2 |
方程为y-2=k(x-
| 2 |
即kx-y+2-
| 2 |
又圆心O到直线l的距离为d=r,
∴
|2-
| ||
|
| 2 |
解得k=
| ||
| 4 |
此时圆的切线方程为
| 2 |
当斜率k不存在时,圆的切线方程为x-
| 2 |
综上,切线l的方程为
| 2 |
| 2 |
点评:本题考查了直线与圆相切的应用问题,解题时通常应用圆心到直线的距离等于半径来解答,是基础题目.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
在正方体ABCD-A1B1C1D1中,下列四队截面中彼此平行的一对是( )
| A、A1BC1与ACD1 |
| B、B1CD1与BDC1 |
| C、B1D1D与BDA1 |
| D、A1DC1与AD1C |
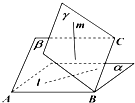 如图,二面角α-AB-β与β-BC-γ均为θ(0<θ<π),AB⊥BC,l?α,m?γ,则下列不可能成立的是( )
如图,二面角α-AB-β与β-BC-γ均为θ(0<θ<π),AB⊥BC,l?α,m?γ,则下列不可能成立的是( )| A、l∥m | B、l⊥m |
| C、m∥AB | D、α⊥γ |
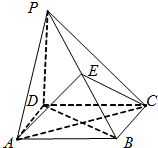 如图,四棱锥P-ABCD的底面ABCD是菱形,∠BAD=60°,PD⊥底面ABCD,点E在棱PB上.
如图,四棱锥P-ABCD的底面ABCD是菱形,∠BAD=60°,PD⊥底面ABCD,点E在棱PB上.