题目内容
在样本频率分布直方图中,共有5个小长方形,若中间一个小长方形的面积等于其他4个小长方形的面积和的
,且样本容量为120,则中间一组的频数为 .
| 1 |
| 3 |
考点:频率分布直方图
专题:概率与统计
分析:由频率分布直方图分析可得“中间一个小长方形”对应的频率,再由频率与频数的关系,中间一组的频数.
解答:
解:设中间一个小长方形的面积为x,其他4个小长方形的面积之和为y,
则有:x=
y,x+y=1,
解得:x=0.25,
∴中间一组的频数=120×0.25=30.
故答案为:30.
则有:x=
| 1 |
| 3 |
解得:x=0.25,
∴中间一组的频数=120×0.25=30.
故答案为:30.
点评:本题是对频率、频数灵活运用的考查,各小组频数之和等于数据总和,各小组频率之和等于1.频率、频数的关系:频率=
.
| 频数 |
| 样本容量 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10盏路灯,为节约用电,关掉其中三盏,不关两端,不连续关灯,(任两盏不连续).则共有( )种方法.
| A、15 | B、20 | C、36 | D、49 |
如图是一个空间几何体的三视图,则该几何体的体积为( )
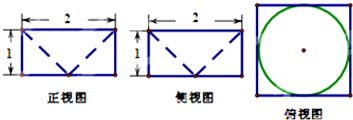

A、4-
| ||
B、8-
| ||
C、4-
| ||
D、8-
|