题目内容
14.函数y=2x3+1的图象与函数y=3x2-b的图象有三个不相同的交点,则实数b的取值范围是( )| A. | (0,2) | B. | (-2,0) | C. | (0,4) | D. | (-1,0) |
分析 设y=f(x)=2x3+1,y=g(x)=3x2-b,根据题意得方程f(x)=g(x)有三个不相等的实数根,进而转化为b=-2x3+3x2-1,对右边对应的函数单调性的讨论,记F(x)=-2x3+3x2-1然后利用导数工具研究其单调性,得到它的极大值与极小值,最后根据这个极值建立关于字母b的不等式组,解之可得实数b的取值范围.
解答 解:设y=f(x)=2x3+1,y=g(x)=3x2-b
∵y=2x3+1的图象与y=3x2-b的图象有三个不相同的交点,
∴方程f(x)=g(x)有三个不相等的实数根
即:2x3+1=3x2-b⇒b=-2x3+3x2-1
记F(x)=-2x3+3x2-1,得F′(x)=-6x(x-1),
∴F(x)在(0,1)递增,在(1,+∞),(-∞,0)上递减,F(0)取极小,F(1)取极大.
所以方程f(x)=g(x)有三个不相等的实数根的充要条件是:
函数F(x)的极大值大于b,而极小值小于b
∴$\left\{\begin{array}{l}{F(0)=-1>b}\\{F(1)=0<b}\end{array}\right.$⇒b∈(-1,0)
故选:D.
点评 本题以多项式函数为载体,考查了方程根的个数知识点,属于中档题.从函数图象联系到方程的根,利用参数分离研究函数单调性的方法解决,是本题解决的特征.

练习册系列答案
相关题目
2.f(x)=$\left\{{\begin{array}{l}{\frac{1}{x}+alnx,(x>0,0<a<e)}\\{cosx,(x≤0)}\end{array}}$,则y=f[f(x)]的零点有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 无穷多个 |
19.设实数x,y满足$\left\{\begin{array}{l}2x-y≥0\\ x+y-3≥0\\ y-x≥0\end{array}\right.$,则z=2x+y的最小值为( )
| A. | $\frac{9}{2}$ | B. | 4 | C. | 3 | D. | 0 |
4.若f(x)是偶函数,且当x∈[0,+∞)时,f(x)=x-1,则f(x)<0的解集是( )
| A. | (-1,0) | B. | (-∞,-1)∪(0,1) | C. | (-1,1) | D. | (0,1) |
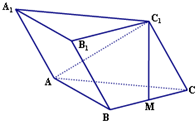 如图,斜三棱柱ABC-A1B1C1的所有棱长均为a,M是BC的中点,侧面B1C1CB⊥底面ABC,且AC1⊥BC.
如图,斜三棱柱ABC-A1B1C1的所有棱长均为a,M是BC的中点,侧面B1C1CB⊥底面ABC,且AC1⊥BC.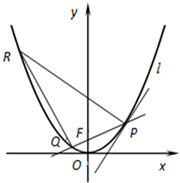 如图,点F是抛物线C:x2=2y的焦点,点P(x1,y1)为抛物线上的动点(P在第一象限),直线PF交抛物线C于另一点Q,直线l与抛物线C相切于点P.过点P作直线l的垂线交抛物线C于点R.
如图,点F是抛物线C:x2=2y的焦点,点P(x1,y1)为抛物线上的动点(P在第一象限),直线PF交抛物线C于另一点Q,直线l与抛物线C相切于点P.过点P作直线l的垂线交抛物线C于点R.