题目内容
4.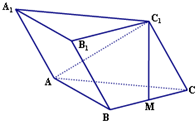 如图,斜三棱柱ABC-A1B1C1的所有棱长均为a,M是BC的中点,侧面B1C1CB⊥底面ABC,且AC1⊥BC.
如图,斜三棱柱ABC-A1B1C1的所有棱长均为a,M是BC的中点,侧面B1C1CB⊥底面ABC,且AC1⊥BC.(Ⅰ)求证:BC⊥C1M;
(Ⅱ)求二面角A1-AB-C的平面角的余弦值.
分析 (Ⅰ)连接AM,由△ABC是正三角形,得AM⊥BC,又AC1⊥BC,可得BC⊥平面AC1M,由此能证明BC⊥C1M.
(Ⅱ)以MB,MA,MC1为x,y,z轴建立空间直角坐标系,求出A,B,A1点的坐标,则$\overrightarrow{A{A}_{1}}$,$\overrightarrow{AB}$可求,设平面A1AB的法向量为$\overrightarrow m=(x,y,z)$,
从而列出方程组,求解可得$\overrightarrow{n}$,由此能求出二面角A1-AB-C的余弦值.
解答 (Ⅰ)证明:连接AM,∵△ABC是正三角形,
∴AM⊥BC,又AC1⊥BC,且AC1∩AM=A,
∴BC⊥平面AC1M,
∴BC⊥C1M.
(Ⅱ)解:以MB,MA,MC1为x,y,z轴建立空间直角坐标系,
则$A(0,\frac{{\sqrt{3}}}{2}a,0),B(\frac{a}{2},0,0),{A_1}(\frac{a}{2},\frac{{\sqrt{3}}}{2}a,\frac{{\sqrt{3}}}{2}a)$,
∴$\overrightarrow{A{A_1}}=(\frac{a}{2},0,\frac{{\sqrt{3}}}{2}a),\overrightarrow{AB}=(\frac{a}{2},-\frac{{\sqrt{3}}}{2}a,0)$.
设平面A1AB的法向量为$\overrightarrow m=(x,y,z)$,
则$\left\{{\begin{array}{l}{\frac{a}{2}x+\frac{{\sqrt{3}a}}{2}z=0}\\{\frac{a}{2}x-\frac{{\sqrt{3}a}}{2}y=0}\end{array}}\right.$,
∴$\overrightarrow m=(\sqrt{3},1,-1)$.
又平面ABC的法向量是$\overrightarrow n=(0,0,1)$,
∴$cos<\overrightarrow m,\overrightarrow n>=-\frac{{\sqrt{5}}}{5}$
∴二面角A1-AB-C的平面角的余弦值为:$-\frac{\sqrt{5}}{5}$.
点评 本题考查异面直线垂直的证明,考查二面角的余弦值的求法,考查计算能力,空间思维能力,是中档题.

| A. | 5$\sqrt{3}$ | B. | 5 | C. | -5$\sqrt{3}$ | D. | 20 |
| A. | (0,2) | B. | (-2,0) | C. | (0,4) | D. | (-1,0) |
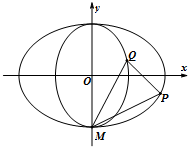 如图,中心在坐标原点,焦点分别在x轴和y轴上的椭圆T1,T2都过点M(0,-$\sqrt{2}$),且椭圆T1与T2的离心率均为$\frac{\sqrt{2}}{2}$.
如图,中心在坐标原点,焦点分别在x轴和y轴上的椭圆T1,T2都过点M(0,-$\sqrt{2}$),且椭圆T1与T2的离心率均为$\frac{\sqrt{2}}{2}$.