题目内容
4.若f(x)是偶函数,且当x∈[0,+∞)时,f(x)=x-1,则f(x)<0的解集是( )| A. | (-1,0) | B. | (-∞,-1)∪(0,1) | C. | (-1,1) | D. | (0,1) |
分析 根据函数奇偶性的性质进行求解即可.
解答 解:当x∈0,+∞)时,f(x)=x-1,此时由f(x)<0得x-1<0,得0≤x<1,
根据偶函数的对称性得当x<0时,f(x)<0得解为-1<x≤0,
综上f(x)<0的解集是(-1,1),
故选:C
点评 本题主要考查不等式的求解,根据偶函数的对称性是解决本题的关键.

练习册系列答案
相关题目
14.函数y=2x3+1的图象与函数y=3x2-b的图象有三个不相同的交点,则实数b的取值范围是( )
| A. | (0,2) | B. | (-2,0) | C. | (0,4) | D. | (-1,0) |
15.已知 f(x)=$\frac{a-{2}^{x}}{1+{2}^{x}}$(a∈R)是奇函数,且实数k满足f(2k-1)<$\frac{1}{3}$,则k的取值范围是( )
| A. | (0,+∞) | B. | (-∞,0) | C. | (-∞,1) | D. | (1,+∞) |
9.函数f(x)=$\left\{\begin{array}{l}{2^{-x}}-1,x≤0\\{x^{\frac{1}{2}}},x>0\end{array}$满足f(x)=1的x值为( )
| A. | 1 | B. | -1 | C. | 1或-2 | D. | 1或-1 |
16.设a=log${\;}_{\frac{1}{2}}$3,b=($\frac{1}{2}$)${\;}^{\frac{1}{3}}$,c=2${\;}^{\frac{1}{3}}$,则( )
| A. | a<b<c | B. | c<b<a | C. | c<a<b | D. | b<a<c? |
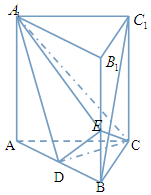 如图,在直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=$\frac{{\sqrt{2}}}{2}$AB.
如图,在直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=$\frac{{\sqrt{2}}}{2}$AB. 如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠D=90°,且AB∥CD,AB=AD,∠BCD=45°.
如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠D=90°,且AB∥CD,AB=AD,∠BCD=45°.