题目内容
3.设$\overrightarrow a$=(1,2),$\overrightarrow b$=(1,1),$\overrightarrow c$=$\overrightarrow a$+k$\overrightarrow b$.若$\overrightarrow b$⊥$\overrightarrow c$,则实数k的值等于$-\frac{3}{2}$.分析 求出向量$\overrightarrow c$,利用向量垂直的充要条件列出方程,求解即可.
解答 解:$\overrightarrow a$=(1,2),$\overrightarrow b$=(1,1),$\overrightarrow c$=$\overrightarrow a$+k$\overrightarrow b$=(1+k,2+k).
若$\overrightarrow b$⊥$\overrightarrow c$,则1+k+2+k=0,
解得k=$-\frac{3}{2}$.
故答案为:-$\frac{3}{2}$.
点评 本题考查向量垂直的充要条件的应用,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.函数y=2x3+1的图象与函数y=3x2-b的图象有三个不相同的交点,则实数b的取值范围是( )
| A. | (0,2) | B. | (-2,0) | C. | (0,4) | D. | (-1,0) |
15.已知 f(x)=$\frac{a-{2}^{x}}{1+{2}^{x}}$(a∈R)是奇函数,且实数k满足f(2k-1)<$\frac{1}{3}$,则k的取值范围是( )
| A. | (0,+∞) | B. | (-∞,0) | C. | (-∞,1) | D. | (1,+∞) |
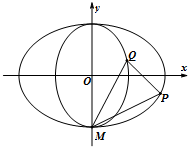 如图,中心在坐标原点,焦点分别在x轴和y轴上的椭圆T1,T2都过点M(0,-$\sqrt{2}$),且椭圆T1与T2的离心率均为$\frac{\sqrt{2}}{2}$.
如图,中心在坐标原点,焦点分别在x轴和y轴上的椭圆T1,T2都过点M(0,-$\sqrt{2}$),且椭圆T1与T2的离心率均为$\frac{\sqrt{2}}{2}$.