题目内容
2.f(x)=$\left\{{\begin{array}{l}{\frac{1}{x}+alnx,(x>0,0<a<e)}\\{cosx,(x≤0)}\end{array}}$,则y=f[f(x)]的零点有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 无穷多个 |
分析 利用导数判断函数的单调性求出函数在x>0时的最小值,判断函数的零点个数,然后判断x≤0时,函数的零点的个数,推出结果即可.
解答 解:当x>0时,求导可得$f(x)=\frac{1}{x}+alnx$在$x=\frac{1}{a}$时有最小值,$f(\frac{1}{a})=a+aln\frac{1}{a}$,
又$0<a<e,ln\frac{1}{a}>ln\frac{1}{e}=-1$,所以$f(\frac{1}{a})>0$,即x>0时,f(x)>0,y=f[f(x)]>0,没有零点.
当x≤0时,cosx∈[-1,1],若cosx>0,则y=f[f(x)]>0,
若cosx∈[-1,0],则同样可得y=f[f(x)]>0,函数没有零点.
故选:A.
点评 本题考查函数的导数的综合应用,函数的零点个数的判断,考查计算能力.

练习册系列答案
相关题目
17.在三棱锥P-ABC中,AB⊥BC,AB=BC=$\sqrt{2}$,PA=PC=2,AC中点为M,cos∠PMB=$\frac{{\sqrt{3}}}{3}$,则此三棱锥的外接球的表面积为( )
| A. | $\frac{3π}{2}$ | B. | 2π | C. | 6π | D. | $\sqrt{6}$π |
14.函数y=2x3+1的图象与函数y=3x2-b的图象有三个不相同的交点,则实数b的取值范围是( )
| A. | (0,2) | B. | (-2,0) | C. | (0,4) | D. | (-1,0) |
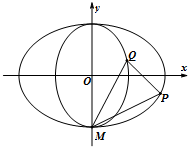 如图,中心在坐标原点,焦点分别在x轴和y轴上的椭圆T1,T2都过点M(0,-$\sqrt{2}$),且椭圆T1与T2的离心率均为$\frac{\sqrt{2}}{2}$.
如图,中心在坐标原点,焦点分别在x轴和y轴上的椭圆T1,T2都过点M(0,-$\sqrt{2}$),且椭圆T1与T2的离心率均为$\frac{\sqrt{2}}{2}$.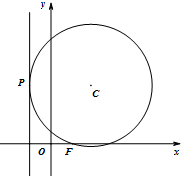 如图,动圆C过点F(1,0),且与直线x=-1相切于点P.
如图,动圆C过点F(1,0),且与直线x=-1相切于点P.