题目内容

已知log127=a，log123=b，试用a、b来表示log2863．
考点：对数的运算性质
专题：函数的性质及应用
分析：根据对数的换底公式即可得到结论．
解答： 解：由log123=b得b=log123=
lg3
lg12
=
lg3
lg3+lg4
即lg4=
1-b
2b
•lg3，
由log127=a得a=log127=
lg7
lg12
，b=
lg3
lg12
，
∴lg7=
a
b
•lg3，
则log2863=
lg63
lg28
=
lg7+lg9
lg4+lg7
=
lg7+2lg3
lg4+lg7
=
a
b
lg3+2lg3
1-b
2b
lg3+
a
b
lg3
=
a
b
+2
1-b
2b
+
a
b
=
2a+4b
1+2a-b
点评：本题主要考查对数的基本运算，利用对数的换底公式是解决本题的关键．
练习册系列答案
相关题目
“m＞3”是“方程
x2
m-1
-
y2
m-3
=1表示双曲线”的（　　）
A、充分不必要条件
B、必要不充分条件
C、充分必要条件
D、既不充分又不必要条件
已知函数f（x）=ln
x
a
，若曲线y=f（x）在（1，f（1））处的切线为x-y-1=0，求a的值．
在△ABC中，a、b、c分别为三个内角∠A、∠B、∠C的对边，已知b2+c2=a2+bc，若sin2A-sin（A-C）=sinB，求∠C的大小．
若集合A={1，a}，集合B={1，3，a2}，且对于?x∈A，都有x∈B，则实数a的取值个数为（　　）
A、1B、2C、3D、4
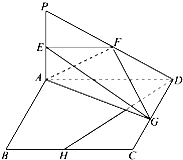如图所示，PA⊥平面ABCD，四边形ABCD为正方形，且AD=2PA，E，F，G，H分别是线段PA，PD，CD，BC的中点．
（Ⅰ）求证：平面FDH⊥平面AEG；
（Ⅱ）求三棱锥E-AFG与四棱锥P-ABCD的体积比．
二项式（a-
1
a
）n的展开式中仅有3项有理项，则n的取值可以是
 
．
若向量
a
与
b
共线，|
a
|=|
b
|=1，则|
a
-
b
|=
 
．
在△ABC中，∠B为直角，P是△ABC外一点，且PA=PB，PB⊥BC．若M是PC的中点，试确定AB上点N的位置，使得MN⊥AB．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网