题目内容
10．已知函数$f（x）=\left\{\begin{array}{l}（a-2）x-1，x≤1\\{log}_{a}^{x}，x＞1\end{array}\right.$． 若f（x）在R上是单调递增函数，则实数a的取值范围是（ ）| A． | （2，3] | B． | （2，3） | C． | （2，+∞） | D． | （1，2） |
分析 根据对数函数以及一次函数的性质求出a的范围即可．
解答 解：对数函数在x＞1时是增函数，所以a＞1，
又f（x）=（a-2）x-1，x≤1是增函数，
∴a＞2，并且x=1时（a-2）x-1≤0，即a-3≤0，
所以2＜a≤3，
故选：A．
点评 本题考查了函数的单调性问题，考查对数函数以及一次函数的性质，是一道基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
6．在各项为正实数的等差数列{an}中，其前2016项的和S2016=1008，则$\frac{1}{{{a_{1001}}}}+\frac{1}{{{a_{1016}}}}$的最小值为（ ）
| A． | 6 | B． | 4 | C． | $\frac{1}{84}$ | D． | $\frac{1}{251}$ |
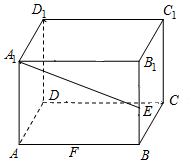已知在长方体ABCD-A1B1C1D1中，AD=AA1=1，AB=2，点F是AB边上动点，点E是棱B1B的中点．
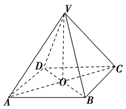如图所示，四棱锥V-ABCD的底面为边长等于2cm的正方形，顶点V与底面正方形中心的连线为棱锥的高，侧棱长VC=4cm，求这个正四棱锥的体积．