题目内容
15.已知f(x)=xlnx.(1)求$g(x)=\frac{f(x)+2}{x}$的单调区间;
(2)若不等式k+2x-e≤f(x)恒成立,求k的取值范围.
分析 (1)求出g(x)的导数,解关于导函数的不等式,求出函数的单调区间即可;
(2)问题转化为k≤xlnx-2x+e恒成立,令h(x)=xlnx-2x+e,(x>0),求出函数的单调区间即可.
解答 解:(1)∵f(x)=xlnx,
∴g(x)=$\frac{xlnx+2}{x}$=lnx+$\frac{2}{x}$,
则g′(x)=$\frac{1}{x}$-$\frac{2}{{x}^{2}}$=$\frac{x-2}{{x}^{2}}$,
令g′(x)>0,解得:x>2,
令g′(x)<0,解得:0<x<2,
故g(x)在(0,2)递减,在(2,+∞)递增,
(2)若不等式k+2x-e≤f(x)恒成立,
则k≤xlnx-2x+e恒成立,
令h(x)=xlnx-2x+e,(x>0),
则h′(x)=lnx-1,
令h′(x)>0,解得:x>e,
令h′(x)<0,解得:0<x<e,
故h(x)在(0,e)递减,在(e,+∞)递增,
故h(x)min=h(e)=0,
故k≤0.
点评 本题考查了函数的单调性、最值问题,考查导数的应用,是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.函数f(x)=log(2x-1)$\sqrt{3x-2}$的定义域是( )
| A. | ($\frac{2}{3}$,+∞) | B. | ($\frac{2}{3}$,1)∪(1,+∞) | C. | ($\frac{1}{2}$,+∞) | D. | ($\frac{1}{2}$,1)∪(1,+∞) |
6.已知函数f(x)=$\frac{x+1}{{e}^{x}-1}$+x(x∈(0,+∞),且f(x)在x0处取得最小值,则以下各式正确的序号为( )
①f(x0)<x0+1 ②f(x0)=x0+1 ③f(x0)>x0+1 ④f(x0)<3 ⑤f(x0)>3.
①f(x0)<x0+1 ②f(x0)=x0+1 ③f(x0)>x0+1 ④f(x0)<3 ⑤f(x0)>3.
| A. | ①④ | B. | ②④ | C. | ②⑤ | D. | ③⑤ |
3.如图所示的几何体,则该几何体的俯视图是选项图中的( )
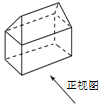

| A. |  | B. |  | C. |  | D. |  |
10.已知函数$f(x)=\left\{\begin{array}{l}(a-2)x-1,x≤1\\{log}_{a}^{x},x>1\end{array}\right.$. 若f(x)在R上是单调递增函数,则实数a的取值范围是( )
| A. | (2,3] | B. | (2,3) | C. | (2,+∞) | D. | (1,2) |
20.下列四个命题中,正确的是( )
| A. | 奇函数的图象一定过原点 | B. | y=x2+1(-4<x≤4)是偶函数 | ||
| C. | y=|x+1|-|x-1|是奇函数 | D. | y=x+1是奇函数 |
7.下列抽样实验中,适合用抽签法的是( )
| A. | 从某工厂生产的3000件产品中抽取600件进行质量检验 | |
| B. | 从某工厂生产的两箱(每箱15件)产品中抽取6件进行质量检验 | |
| C. | 从甲、乙两厂生产的两箱(每箱15件)产品中抽取6件进行质量检验 | |
| D. | 从某厂生产的3000件产品中抽取10件进行质量检验 |