题目内容
将号码分别为1,2,…,8的八个小球放入一个袋中,这些小球仅号码不同,其余完全相同,甲从袋中摸出一个球,其号码为x,放回后乙从此袋中在摸出一个球,其中号码为y,则不等式x+2y-10<0成立的事件发生的概率等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:等可能事件的概率,列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:每次摸出的号码(a,b)共有 8×8=64个,满足x+2y-10<0的共有4个,由此使不等式x+2y-10<0成立的事件发生的概率
解答:
 解:每次摸出的号码(a,b)共有 8×8=64个,
解:每次摸出的号码(a,b)共有 8×8=64个,
其中满足x+2y-10<0(即红色的点)共有16个,如图所示
不等式x+2y-10<0成立的事件发生的概率等于P=
=
故选:A
 解:每次摸出的号码(a,b)共有 8×8=64个,
解:每次摸出的号码(a,b)共有 8×8=64个,其中满足x+2y-10<0(即红色的点)共有16个,如图所示
不等式x+2y-10<0成立的事件发生的概率等于P=
| 16 |
| 64 |
| 1 |
| 4 |
故选:A
点评:本题主要考查等可能事件的概率,关键是求出满足x+2y-10<0成立的基本事件,采用建立坐标系,根据点的坐标的问题,求出满足条件的点,属于基础题

练习册系列答案
相关题目
命题“若x>0,则x2>0”的否命题是( )
| A、若x>0,则x2≤0 |
| B、若x2>0,则x>0 |
| C、若x≤0,则x2≤0 |
| D、若x2≤0,则x≤0 |
函数y=
的定义域是( )
| 1 |
| x-2 |
| A、{x|x<2} |
| B、{x|x>2} |
| C、{x|x≠2} |
| D、{x|x≠0} |
给出下列随机变量:
①某网站一天内的点击数;
②抽检一件产品的真实重量与标准重量的误差;
③某地区下个月降雨的天数;
④一个沿数轴进行随机运动的质点,它在数轴上的位置X.
其中是离散型随机变量的是( )
①某网站一天内的点击数;
②抽检一件产品的真实重量与标准重量的误差;
③某地区下个月降雨的天数;
④一个沿数轴进行随机运动的质点,它在数轴上的位置X.
其中是离散型随机变量的是( )
| A、①③ | B、②④ | C、①④ | D、②③ |
已知函数f(x)=
,f2(x)=f(x),fn+1(x)=f(fn(x)),x∈N+,则f2015(x)=( )
| 1 |
| 1-x |
| A、x | ||
B、
| ||
C、
| ||
D、
|
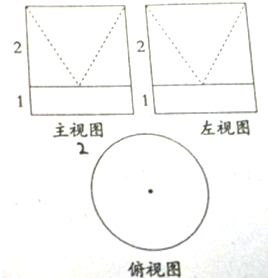 如图是无上底的几何体的三视图,其中正视图和侧视图是全等的图形,外边界是矩形,它的底边长为4,宽为3,俯视图是半径为2的圆,求该几何体的表面积和体积.
如图是无上底的几何体的三视图,其中正视图和侧视图是全等的图形,外边界是矩形,它的底边长为4,宽为3,俯视图是半径为2的圆,求该几何体的表面积和体积.