题目内容
20．已知倾斜角为θ的直线，与直线x-3y+1=0垂直，则tanθ=（ ）| A． | $\frac{1}{3}$ | B． | 3 | C． | -3 | D． | $-\frac{1}{3}$ |
分析 利用直线相互垂直的充要条件即可得出．
解答 解：∵倾斜角为θ的直线，与直线x-3y+1=0垂直，
∴$-\frac{1}{-3}$×tanθ=-1，
解得tanθ=-3．
故选：C．
点评 本题考查了直线相互垂直的充要条件，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
10．阅读如图所示的程序框图，若输入m=2016，则输出S等于（ ）
| A． | 10072 | B． | 10082 | C． | 10092 | D． | 20102 |
11．已知数列{an}中，a1=25，4an+1=4an-7，若用Sn表示该数列前n项和，则（ ）
| A． | 当n=15时，Sn取到最大值 | B． | 当n=16时，Sn取到最大值 | ||
| C． | 当n=15时，Sn取到最小值 | D． | 当n=16，Sn取到最小值 |
8．从5位男教师和3为女教师中选出3位教师，派往郊区3所学校支教，每校1人．要求这3位教师中男、女教师都要有，则不同的选派方案共有（ ）
| A． | 250种 | B． | 450种 | C． | 270种 | D． | 540种 |
15．函数f（x）=$\frac{4-x}{4x-2}$，在区间（0，$\frac{1}{2}$）∪（$\frac{1}{2}$，2）上函数f（x）≥1的概率为（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{7}{20}$ | C． | $\frac{9}{20}$ | D． | $\frac{1}{2}$ |
5．已知函数$f（x）=\frac{1}{3}a{x^3}-\frac{1}{2}b{x^2}+x$，连续抛掷两颗骰子得到的点数分别是a，b，则函数f′（x）在x=1处取得最值的概率是（ ）
| A． | $\frac{1}{36}$ | B． | $\frac{1}{18}$ | C． | $\frac{1}{12}$ | D． | $\frac{1}{6}$ |
12．已知函数f（x）=$\frac{{e}^{x}-{e}^{-x}}{{e}^{x}+{e}^{-x}}$，则不等式f（log2x）-f（log${\;}_{\frac{1}{2}}$x）≥$\frac{2（{e}^{2}-1）}{{e}^{2}+1}$的解集为（ ）
| A． | [$\frac{1}{2}$，+∞） | B． | [2，+∞） | C． | （0，2] | D． | [$\frac{1}{2}$，2] |
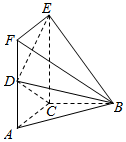如图，矩形ACEF所在的平面与Rt△ABC所在的平面垂直，D是AF的中点，且AC=BC=AD=$\frac{1}{2}$CE．