题目内容
2.已知2a+b=2,求f(x)=4a+2b的最值,及此时a,b的值.分析 利用基本不等式的性质、指数函数的性质即可得出.
解答 解:∵2a+b=2,
∴f(x)=4a+2b≥2$\sqrt{{4}^{a}•{2}^{b}}$=2$\sqrt{{2}^{2a+b}}$=2$\sqrt{{2}^{2}}$=4,当且仅当2a=b=1时取等号.
点评 本题考查了基本不等式的性质、指数函数的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
12.已知函数f(x)=$\frac{{e}^{x}-{e}^{-x}}{{e}^{x}+{e}^{-x}}$,则不等式f(log2x)-f(log${\;}_{\frac{1}{2}}$x)≥$\frac{2({e}^{2}-1)}{{e}^{2}+1}$的解集为( )
| A. | [$\frac{1}{2}$,+∞) | B. | [2,+∞) | C. | (0,2] | D. | [$\frac{1}{2}$,2] |
14.若实数x,y满足x2+y2-2x+2$\sqrt{3}$y+3=0,则x-$\sqrt{3}$y的取值范围是( )
| A. | [2,+∞) | B. | (2,6) | C. | [2,6] | D. | [-4,0] |
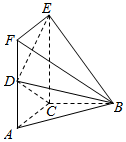 如图,矩形ACEF所在的平面与Rt△ABC所在的平面垂直,D是AF的中点,且AC=BC=AD=$\frac{1}{2}$CE.
如图,矩形ACEF所在的平面与Rt△ABC所在的平面垂直,D是AF的中点,且AC=BC=AD=$\frac{1}{2}$CE.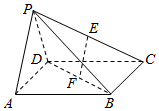 如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,E、F分别为PC、BD的中点,平面PAD⊥平面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$AD.
如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,E、F分别为PC、BD的中点,平面PAD⊥平面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$AD.