题目内容
3．
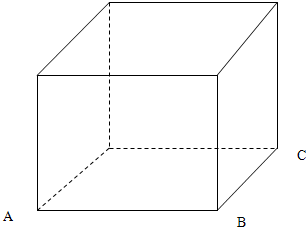如图，正方体ABCD-A1B1C1D1的棱上到AB，CC1的距离相等的所有点的个数为4．
分析 结合正方体中线面、线线垂直，先找定点、再找棱的中点，找出符合条件的所有的点．
解答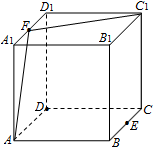 
解：如图：正方体ABCD-A1B1C1D1，E、F分别是BC和A1D1的中点，连接AF和FC1，
根据正方体的性质知，BB1⊥AB，C1C⊥B1C1，故B1到异面直线AB，CC1的距离相等，
同理可得，D到异面直线AB，CC1的距离相等，
又有AB⊥BC，C1C⊥BC，故E到异面直线AB，CC1的距离相等，
F 为A1D1的中点，易计算FA=FC1，故F到异面直线AB，CC1的距离相等，共有4个点．
故答案为4．
点评 本题考查了正方体体的结构特征，考查了线面、线线垂直定理的应用，利用异面直线之间距离的定义进行判断，考查了观察能力和空间想象能力．
练习册系列答案
口算题天天练系列答案
相关题目
1．
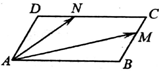如图，在平行四边形ABCD中，$∠BAD=\frac{π}{3}$，AB=2，AD=1，若M、N分别是边BC、CD上的点，且满足$\frac{BM}{BC}=\frac{NC}{DC}=λ$，其中λ∈[0，1]，则$\overrightarrow{AM}•\overrightarrow{AN}$的取值范围是（ ）
如图，在平行四边形ABCD中，$∠BAD=\frac{π}{3}$，AB=2，AD=1，若M、N分别是边BC、CD上的点，且满足$\frac{BM}{BC}=\frac{NC}{DC}=λ$，其中λ∈[0，1]，则$\overrightarrow{AM}•\overrightarrow{AN}$的取值范围是（ ）| A． | [0，3] | B． | [1，4] | C． | [2，5] | D． | [1，7] |
14．方程xy2+x2y=1所表示的曲线（ ）
| A． | 关于x轴对称 | B． | 关于y轴对称 | C． | 关于原点对称 | D． | 关于直线y=x对称 |
8．一个几何体的三视图如图所示，则这个几何体的体积是（ ）
| A． | 2 | B． | $\frac{1}{2}$ | C． | 3 | D． | $\frac{1}{3}$ |
15．已知函数y=f（x）的图象关于直线x=-1对称，且当x∈（0，+∞）时，有f（x）=$\frac{1}{x}$，当x∈（-∞，-2）时，f（x）的解析式为（ ）
| A． | f（x）=-$\frac{1}{x}$ | B． | f（x）=-$\frac{1}{x-2}$ | C． | f（x）=$\frac{1}{x+2}$ | D． | f（x）=-$\frac{1}{x+2}$ |