题目内容
12.已知函数f(x)=2ax2+4x-3-a,a∈R.(1)当a=1时,求函数f(x)在[-1,1]上的最大值;
(2)如果函数f(x)在R上有两个不同的零点,求a的取值范围.
分析 (1)当a=1时,f(x)=2x2+4x-4,分析x∈[-1,1]时的单调性,可得函数f(x)在[-1,1]上的最大值;
(2)如果函数f(x)在R上有两个不同的零点,则$\left\{\begin{array}{l}a≠0\\△>0\end{array}\right.$,解得a的取值范围.
解答 解:(1)当a=1时,f(x)=2x2+4x-4
=2(x+1)2-6.
因为x∈[-1,1]时,函数为增函数,
所以x=1时,f(x)取最大值f(1)=2.
(2)∵如果函数f(x)在R上有两个不同的零点,
∴$\left\{\begin{array}{l}a≠0\\△>0\end{array}\right.$,即$\left\{\begin{array}{l}a≠0\\ 16+8a(a+3)>0\end{array}\right.$
∴a<-2或-1<a<0或a>0,
∴a的取值范围是(-∞,-2)∪(-1,0)∪(0,+∞).
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
20.0<x<2是不等式|x+1|<3成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
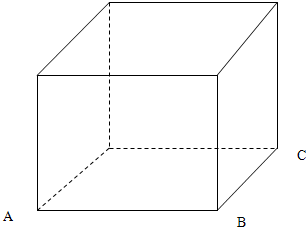 如图,正方体ABCD-A1B1C1D1的棱上到AB,CC1的距离相等的所有点的个数为4.
如图,正方体ABCD-A1B1C1D1的棱上到AB,CC1的距离相等的所有点的个数为4. 为打击索马里海盗,保护各国商船的顺利通行,我海军某部奉命前往该海域执行护航任务,某天我护航舰正在某小岛A北偏西45°并距该岛20海里的B处待命,位于该岛正西方向C处的某外国商船遭到海盗袭击,船长发现在其北偏东60°的方向有我军护航舰(如图所示),便发出紧急求救信号,我护航舰接警后,立即沿BC航线以每小时60海里的速度前去救援,问我护航舰需多少分钟可以到达该商船所在的位置C处?(结果精确到个位,参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
为打击索马里海盗,保护各国商船的顺利通行,我海军某部奉命前往该海域执行护航任务,某天我护航舰正在某小岛A北偏西45°并距该岛20海里的B处待命,位于该岛正西方向C处的某外国商船遭到海盗袭击,船长发现在其北偏东60°的方向有我军护航舰(如图所示),便发出紧急求救信号,我护航舰接警后,立即沿BC航线以每小时60海里的速度前去救援,问我护航舰需多少分钟可以到达该商船所在的位置C处?(结果精确到个位,参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)