题目内容
11.已知数列{an}满足a1=$\frac{7}{8}$,且an+1=$\frac{1}{2}$an+$\frac{1}{3}$,n∈N*.(1)求证:{an-$\frac{2}{3}$}是等比数列;
(2)求数列{an}的通项公式.
分析 (1)对an+1=$\frac{1}{2}$an+$\frac{1}{3}$进行变形处理得到:an+1-$\frac{2}{3}$=$\frac{1}{2}$an-$\frac{1}{3}$=$\frac{1}{2}$(an-$\frac{2}{3}$),根据等比数列的性质证得结论;
(2)根据{an-$\frac{2}{3}$}是以$\frac{5}{24}$为首项,$\frac{1}{2}$为公比的等比数列来推知数列{an}的通项公式.
解答 (1)证明:由已知得:an+1-$\frac{2}{3}$=$\frac{1}{2}$an-$\frac{1}{3}$=$\frac{1}{2}$(an-$\frac{2}{3}$),
因为a1=$\frac{7}{8}$,
所以a1-$\frac{2}{3}$=$\frac{5}{24}$,
所以{an-$\frac{2}{3}$}是以$\frac{5}{24}$为首项,$\frac{1}{2}$为公比的等比数列;
(2)解:由(1)知,{an-$\frac{2}{3}$}是以$\frac{5}{24}$为首项,$\frac{1}{2}$为公比的等比数列,
所以an-$\frac{2}{3}$=$\frac{5}{24}$•($\frac{1}{2}$)n-1,
所以an=$\frac{5}{24}$•($\frac{1}{2}$)n-1+$\frac{2}{3}$.
点评 本题考查数列递推式,考查构造法证明等比数列,考查数列的通项,解题的关键是构造法证明等比数列.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
19. 一个正三棱柱的侧棱长和底面边长都相等,它的俯视图如图所示,左视图是一个矩形,棱柱的体积为2$\sqrt{3}$,则这个三棱柱的表面积为( )
一个正三棱柱的侧棱长和底面边长都相等,它的俯视图如图所示,左视图是一个矩形,棱柱的体积为2$\sqrt{3}$,则这个三棱柱的表面积为( )
 一个正三棱柱的侧棱长和底面边长都相等,它的俯视图如图所示,左视图是一个矩形,棱柱的体积为2$\sqrt{3}$,则这个三棱柱的表面积为( )
一个正三棱柱的侧棱长和底面边长都相等,它的俯视图如图所示,左视图是一个矩形,棱柱的体积为2$\sqrt{3}$,则这个三棱柱的表面积为( )| A. | 2$\sqrt{3}$ | B. | 12 | C. | 2$\sqrt{3}$+12 | D. | 2$\sqrt{3}$+6 |
20.0<x<2是不等式|x+1|<3成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
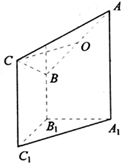 如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知∠A1B1C1=90°,AA1=4,BB1=2,CC1=3,A1B1=B1C1=1.
如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知∠A1B1C1=90°,AA1=4,BB1=2,CC1=3,A1B1=B1C1=1.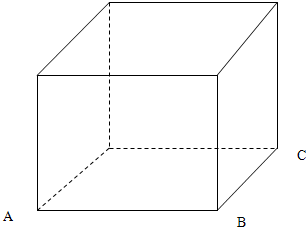 如图,正方体ABCD-A1B1C1D1的棱上到AB,CC1的距离相等的所有点的个数为4.
如图,正方体ABCD-A1B1C1D1的棱上到AB,CC1的距离相等的所有点的个数为4.