题目内容
设复数z=
，若az+b=1+i，求实数a，b的值．
| (1+i)2+3(1-i) |
| 2+i |
考点：复数代数形式的乘除运算
专题：数系的扩充和复数
分析：利用复数的混合运算，化简复数z，然后代入等式，利用复数相等求a，b．
解答：
解：由已知，z=
=
=
=
=1-i，
∴az+b=a（1-i）+b=a+b-ai=1+i，
∴
，
解得a=-1，b=2．
| 2i+3-3i |
| 2+i |
| 3-i |
| 2+i |
| (3-i)(2-i) |
| 5 |
| 5-5i |
| 5 |
∴az+b=a（1-i）+b=a+b-ai=1+i，
∴
|
解得a=-1，b=2．
点评：本题考查了复数的运算以及利用复数相等求参数；如果复数相等，那么它们的实部和虚部分别相等．
练习册系列答案
相关题目
下列命题错误的是（ ）
| A、命题“若m＞0，则方程x2+x-m=0有实数根”的逆否命题为：“若方程x2+x-m=0无实数根，则m≤0” |
| B、“x=1”是“x2-3x+2=0”的充分不必要条件 |
| C、若p且q为假命题，则p，q均为假命题 |
| D、空间中，没有公共点的两直线不一定平行 |
一枚均匀硬币连掷两次，只有一次出现正面的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
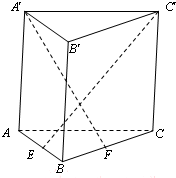如图，直三棱柱ABC-A′B′C′的侧棱长为3，AB⊥BC，且AB=BC=3，点E，F分别是棱AB，BC上的动点，且AE=BF，