题目内容
点（1，-1）到直线3x-4y+3=0的距离为（ ）
| A、2 | ||
| B、1 | ||
C、
| ||
D、
|
考点：点到直线的距离公式
专题：直线与圆
分析：利用点到直线的距离公式求解．
解答：
解：点（1，-1）到直线3x-4y+3=0的距离：
d=
=2．
故选：A．
d=
| |3+4+3| | ||
|
故选：A．
点评：本题考查点到直线的距离的求法，是基础题，解题时要认真审题，注意点到直线的距离公式的合理运用．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
执行如图所示的程序框图，则输出的y值是（ ）
| A、4 | ||
B、
| ||
C、
| ||
| D、-1 |
复数Z=1+（2-sinθ）i在复平面内对应的点所在象限为（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
如图，∠B=∠D，AE⊥BC，∠ACD=90°，且AB=6，AC=4，AD=12，则BE=（ ）
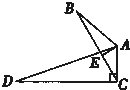
| A、3 | ||
| B、4 | ||
C、4
| ||
| D、5 |
下列命题错误的是（ ）
| A、命题“若m＞0，则方程x2+x-m=0有实数根”的逆否命题为：“若方程x2+x-m=0无实数根，则m≤0” |
| B、“x=1”是“x2-3x+2=0”的充分不必要条件 |
| C、若p且q为假命题，则p，q均为假命题 |
| D、空间中，没有公共点的两直线不一定平行 |
已知O为极点，曲线C1，C2都在极轴的上方，极坐标方程为C1：ρ=2cosθ（0≤θ≤π），C2：ρ=2（0≤θ≤π）．若直线θ=α（ρ∈R，0≤α＜π）与曲线C1，C2交于M，N（M不同于点O）两点，则OM2+MN2的最小值为（ ）
| A、1 | B、2 | C、3 | D、4 |
设动点P（x，y）满足：
=|x+y-2|，则点P的轨迹为（ ）
| 2x2+2(y-2)2 |
| A、直线 | B、抛物线 |
| C、椭圆 | D、双曲线 |
已知i是虚数单位，则复数z=
所对应的点落在（ ）
| i |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |