题目内容
已知e=2.71828…是自然对数的底数.
(Ⅰ)求函数f(x)=ln(x+1)-x+
在[0,+∞)上的最小值;
(Ⅱ)比较ln2和
的大小.
(Ⅰ)求函数f(x)=ln(x+1)-x+
| x2 |
| 2 |
(Ⅱ)比较ln2和
| 13 |
| 20 |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)由已知可得f′(x)=
-1+x,当x∈[0,+∞)时f′(x)≥0,得函数f(x)在[0,+∞)上单调性,即可得到函数的最小值;
(Ⅱ)可用分析法比较ln2和
的大小.
| 1 |
| x+1 |
(Ⅱ)可用分析法比较ln2和
| 13 |
| 20 |
解答:
解:(Ⅰ)由于函数f(x)=ln(x+1)-x+
,
则f′(x)=
-1+x
,
故当x∈[0,+∞)时f′(x)≥0,
则函数f(x)在[0,+∞)上是增函数,
故函数f(x)=ln(x+1)-x+
在[0,+∞)上的最小值为0;
(Ⅱ)可知ln2>
(用分析法比较ln2和
的大小)
下面给出证明:ln2>
,只需证ln4>
,
只需证ln
>
,
而由(Ⅰ)知ln(x+1)≥x-
(x≥0)
所以ln[1+(
-1)]≥(
-1)-
(
-1)2
只需证(
-1)-
(
-1)2>
,
即需证明4(e-1)>0.9e2
而e=2.71828…是自然对数的底数,
故4(e-1)>0.9e2恒成立,
从而ln2>
得证
| x2 |
| 2 |
则f′(x)=
| 1 |
| x+1 |
| x2 |
| x+1 |
故当x∈[0,+∞)时f′(x)≥0,
则函数f(x)在[0,+∞)上是增函数,
故函数f(x)=ln(x+1)-x+
| x2 |
| 2 |
(Ⅱ)可知ln2>
| 13 |
| 20 |
| 13 |
| 20 |
下面给出证明:ln2>
| 13 |
| 20 |
| 13 |
| 10 |
只需证ln
| 4 |
| e |
| 3 |
| 10 |
而由(Ⅰ)知ln(x+1)≥x-
| x2 |
| 2 |
所以ln[1+(
| 4 |
| e |
| 4 |
| e |
| 1 |
| 2 |
| 4 |
| e |
只需证(
| 4 |
| e |
| 1 |
| 2 |
| 4 |
| e |
| 3 |
| 10 |
即需证明4(e-1)>0.9e2
而e=2.71828…是自然对数的底数,
故4(e-1)>0.9e2恒成立,
从而ln2>
| 13 |
| 20 |
点评:本题考查函数在闭区间上的最值的求法,解题时要注意导数性质的合理运用,以及不等式证明中的分析法的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知cos(α-
)=
,
<α<π,则sin(α+
)=( )
| π |
| 2 |
| 3 |
| 5 |
| π |
| 2 |
| π |
| 4 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
已知点 M(x,y)的坐标满足
,N点的坐标为(1,-3),点 O为坐标原点,则
•
的最小值是( )
|
| ON |
| OM |
| A、12 | B、5 | C、-6 | D、-21 |
下列结论中正确的是( )
| A、Z⊆N⊆Q⊆R⊆C |
| B、N⊆Z⊆Q⊆C⊆R |
| C、N⊆Z⊆Q⊆R⊆C |
| D、R⊆N⊆Z⊆Q⊆C |
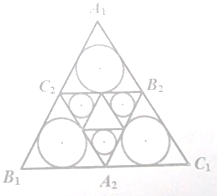 设正三角形A1B1C1边长为a,分别取B1C1,C1A1,A1B1的中点A2,B2,C2,记a1是正三角形A1B1C1除去△A2B2C2后剩下的三个内切圆面积之和,依此类推:记an是△AnBnCn除去△An+1Bn+1Cn+1后剩下的三个三角形内切圆面积之和,从而得到数列{an},设这个数列{an}的前n项和Sn.
设正三角形A1B1C1边长为a,分别取B1C1,C1A1,A1B1的中点A2,B2,C2,记a1是正三角形A1B1C1除去△A2B2C2后剩下的三个内切圆面积之和,依此类推:记an是△AnBnCn除去△An+1Bn+1Cn+1后剩下的三个三角形内切圆面积之和,从而得到数列{an},设这个数列{an}的前n项和Sn.