题目内容
{an}满足a1=4,且an=4-
(n>1),记bn=
.
(1)求证:{bn}为等差数列.
(2)求{an}的通项公式.
| 4 |
| an-1 |
| 1 |
| an-2 |
(1)求证:{bn}为等差数列.
(2)求{an}的通项公式.
考点:数列递推式,等差关系的确定
专题:等差数列与等比数列
分析:(1)由已知得an-2=2-
=2×
,从而
=
+
,进而bn=
+bn-1,由此能证明{bn}为等差数列,公差为
.
(2)由b1=
=
,得bn=
+(n-1)×
=
,由此能求出an=
+2.
| 4 |
| an-1 |
| an-1-2 |
| an-1 |
| 1 |
| an-2 |
| 1 |
| 2 |
| 1 |
| an-1-2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)由b1=
| 1 |
| a1-2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| n |
| 2 |
| 2 |
| n |
解答:
(1)证明:∵{an}满足a1=4,且an=4-
(n>1),
∴an-2=2-
=2×
,
=
+
,
∵bn=
,∴bn=
+bn-1,
∴bn-bn-1=
,
∴{bn}为等差数列,公差为
.
(2)解:b1=
=
,
∴bn=
+(n-1)×
=
,
∴
=
,
∴an=
+2.
| 4 |
| an-1 |
∴an-2=2-
| 4 |
| an-1 |
| an-1-2 |
| an-1 |
| 1 |
| an-2 |
| 1 |
| 2 |
| 1 |
| an-1-2 |
∵bn=
| 1 |
| an-2 |
| 1 |
| 2 |
∴bn-bn-1=
| 1 |
| 2 |
∴{bn}为等差数列,公差为
| 1 |
| 2 |
(2)解:b1=
| 1 |
| a1-2 |
| 1 |
| 2 |
∴bn=
| 1 |
| 2 |
| 1 |
| 2 |
| n |
| 2 |
∴
| 1 |
| an-2 |
| n |
| 2 |
∴an=
| 2 |
| n |
点评:本题考查等差数列的证明,考查数列的通项公式的求法,是中档题,解题时要注意构造法的合理运用.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
执行如图所示的程序框图,则该程序运行后输出的k的值是( )


| A、3 | B、4 | C、5 | D、6 |
sin600°+tan(-300°)的值是( )
A、-
| ||||
B、
| ||||
C、-
|
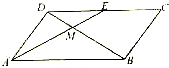 如图,在平行四边形ABCD中,E为DC的中点,AE与BD交于点E,AB=
如图,在平行四边形ABCD中,E为DC的中点,AE与BD交于点E,AB=