题目内容
1.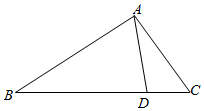 如图,在△ABC中,角A,B,C所对的边为a,b,c,满足sin2A+sin2C-sin2B=$\sqrt{3}$sinA•sinC
如图,在△ABC中,角A,B,C所对的边为a,b,c,满足sin2A+sin2C-sin2B=$\sqrt{3}$sinA•sinC(Ⅰ)求角B;
(Ⅱ)点D在线段BC上,满足DA=DC,且a=11,cos(A-C)=$\frac{\sqrt{5}}{5}$,求线段DC的长.
分析 (Ⅰ)根据正弦定理以及余弦定理可得cosB=$\frac{\sqrt{3}}{2}$,即可求出B的值,
(Ⅱ)根据正弦定理和三角形的关系即可求出答案.
解答 解:(Ⅰ)由正弦定理及sin2A+sin2C-sin2B=$\sqrt{3}$sinA•sinC可得,
a2+c2-b2=$\sqrt{3}$ac,
∴cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{\sqrt{3}}{2}$,
∵B∈(0,π),
(Ⅱ)由条件∠BAD=∠A-∠C,
由cos(A-C)=$\frac{\sqrt{5}}{5}$可得sin(A-C)=$\frac{2\sqrt{5}}{5}$,
设AD=x,则CD=x,BD=11-x,
在△ABD中,由正弦定理得$\frac{BD}{sin∠BAD}$=$\frac{AD}{sinB}$,
故$\frac{11-x}{\frac{2\sqrt{5}}{5}}$=$\frac{x}{\frac{1}{2}}$,解得x=4$\sqrt{5}$-5,
所以AD=DC=4$\sqrt{5}$-5
点评 本题考查了正弦定理和余弦定理,考查了学生的运算能力,属于基础题.

练习册系列答案
相关题目
12.某一算法框图如图所示,则输出的S值为( )
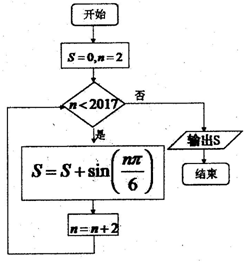

| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\sqrt{3}$ | D. | 0 |
6.已知$\overrightarrow{a}$,$\overrightarrow{b}$为单位向量,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{3}$,则$\overrightarrow{a}$与$\overrightarrow{a}$-$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
13.若复数z满足z2=-4,则|1+z|=( )
| A. | 3 | B. | $\sqrt{3}$ | C. | 5 | D. | $\sqrt{5}$ |
10.已知命题p∧q是假命题,p∨q是真命题,则下列命题一定是真命题的是( )
| A. | p | B. | (¬p)∧(¬q) | C. | q | D. | (¬p)∨(¬q) |