题目内容
16.函数y=-2cos2x+cosx+1,x∈[-$\frac{π}{2}$,$\frac{π}{2}$]的图象大致为( )| A. | 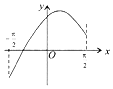 | B. | 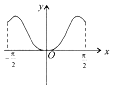 | C. | 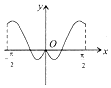 | D. | 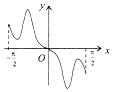 |
分析 根据函数的奇偶性和函数的最值即可求出答案.
解答 解:因为函数y=-2cos2x+cosx+1,x∈[-$\frac{π}{2}$,$\frac{π}{2}$],
所以函数为偶函数,故排除A,D
y=-2cos2x+cosx+1=-2(cosx-$\frac{1}{4}$)2+$\frac{9}{8}$,x∈[-$\frac{π}{2}$,$\frac{π}{2}$],
因为cosx≤1,
所以当cosx=$\frac{1}{4}$时,ymax=$\frac{9}{8}$,当cosx=1时,ymin=0,
故排除C,
故选:B
点评 本题考查了函数图象的识别,关键掌握函数的单调性和函数的最值,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.已知$\overrightarrow a=({sin\frac{ω}{2}x,sinωx}),\overrightarrow b=({sin\frac{ω}{2}x,\frac{1}{2}})$,其中ω>0,若函数$f(x)=\overrightarrow a•\overrightarrow b-\frac{1}{2}$在区间(π,2π)内没有零点,则ω的取值范围是( )
| A. | $({0,\frac{1}{8}}]$ | B. | $({0,\frac{5}{8}}]$ | C. | $({0,\frac{1}{8}}]∪[{\frac{5}{8},1}]$ | D. | $({0,\frac{1}{8}}]∪[{\frac{1}{4},\frac{5}{8}}]$ |
11.已知集合M={x|1<x≤3},若N={x|2<x≤5},则M∪N=( )
| A. | {x|1<x≤5} | B. | {x|2<x≤3} | C. | {x|1≤x<2或3≤x≤5}} | D. | {x|1≤x≤5} |
8. 执行右边的程序框图,若输入?=0.01,则输出的e精确到?的近似值为( )
执行右边的程序框图,若输入?=0.01,则输出的e精确到?的近似值为( )
 执行右边的程序框图,若输入?=0.01,则输出的e精确到?的近似值为( )
执行右边的程序框图,若输入?=0.01,则输出的e精确到?的近似值为( )| A. | 2.69 | B. | 2.70 | C. | 2.71 | D. | 2.72 |
5.在等比数列{an}中,若a1=2,a4=16,则{an}的前5项和S5等于( )
| A. | 30 | B. | 31 | C. | 62 | D. | 64 |
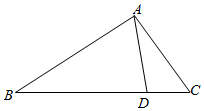 如图,在△ABC中,角A,B,C所对的边为a,b,c,满足sin2A+sin2C-sin2B=$\sqrt{3}$sinA•sinC
如图,在△ABC中,角A,B,C所对的边为a,b,c,满足sin2A+sin2C-sin2B=$\sqrt{3}$sinA•sinC