题目内容
16.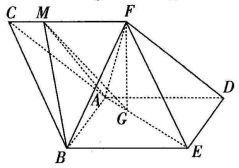 如图,三棱柱ABC-DEF中,侧面ABED是边长为2的菱形,且∠ABE=$\frac{π}{3}$,BC=$\frac{\sqrt{21}}{2}$,四棱锥F-ABED的体积为2,点F在平面ABED内的正投影为G,且G在AE上,点M是在线段CF上,且CM=$\frac{1}{4}$CF.
如图,三棱柱ABC-DEF中,侧面ABED是边长为2的菱形,且∠ABE=$\frac{π}{3}$,BC=$\frac{\sqrt{21}}{2}$,四棱锥F-ABED的体积为2,点F在平面ABED内的正投影为G,且G在AE上,点M是在线段CF上,且CM=$\frac{1}{4}$CF.(Ⅰ)证明:直线GM∥平面DEF;
(Ⅱ)求二面角M-AB-F的余弦值.
分析 (Ⅰ)由四棱锥锥F-ABED的体积为2求出FG,进一步求得EG,可得点G是靠近点A的四等分点.过点G作GK∥AD交DE于点K,可得GK=$\frac{3}{4}AD=\frac{3}{4}CF$.又MF=$\frac{3}{4}CF$,得到MF=GK且MF∥GK.则四边形MFKG为平行四边形,从而得到GM∥FK,进一步得到直线GM∥平面DEF;
(Ⅱ)设AE、BD的交点为O,OB所在直线为x轴,OE所在直线为y轴,点O作平面ABED的垂线为z轴,建立空间直角坐标系,求出平面ABM,ABF的法向量,由两法向量所成角的余弦值得二面角M-AB-F的余弦值.
解答 (Ⅰ)证明:∵四棱锥锥F-ABED的体积为2,
即VF-ABCD=$\frac{1}{3}×\frac{\sqrt{3}}{4}×4×FG=2$,∴FG=$\sqrt{3}$.
又BC=EF=$\frac{\sqrt{21}}{2}$,∴EG=$\frac{3}{2}$,即点G是靠近点A的四等分点.
过点G作GK∥AD交DE于点K,∴GK=$\frac{3}{4}AD=\frac{3}{4}CF$.
又MF=$\frac{3}{4}CF$,∴MF=GK且MF∥GK.
四边形MFKG为平行四边形,
∴GM∥FK,
∴直线GM∥平面DEF;
(Ⅱ)设AE、BD的交点为O,OB所在直线为x轴,OE所在直线为y轴,
过点O作平面ABED的垂线为z轴,建立空间直角坐标系,如图所示:
A(0,-1,0),B($\sqrt{3}$,0,0),F(0,-$\frac{1}{2}$,$\sqrt{3}$),M($\frac{3\sqrt{3}}{4},-\frac{5}{4},\sqrt{3}$).
$\overrightarrow{BA}=(-\sqrt{3},-1,0)$,$\overrightarrow{BM}=(-\frac{\sqrt{3}}{4},-\frac{5}{4},\sqrt{3})$,$\overrightarrow{BF}=(-\sqrt{3},-\frac{1}{2},\sqrt{3})$.
设平面ABM,ABF的法向量分别为$\overrightarrow{m}=({x}_{1},{y}_{1},{z}_{1})$,$\overrightarrow{n}=({x}_{2},{y}_{2},{z}_{2})$.
由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{BA}=0}\\{\overrightarrow{m}•\overrightarrow{BM}=0}\end{array}\right.$,则$\left\{\begin{array}{l}{-\sqrt{3}{x}_{1}-{y}_{1}=0}\\{-\frac{\sqrt{3}}{4}{x}_{1}-\frac{5}{4}{y}_{1}+\sqrt{3}{z}_{1}=0}\end{array}\right.$,取y=-$\sqrt{3}$,得$\overrightarrow{m}=(1,-\sqrt{3},-1)$,
同理求得$\overrightarrow{n}=(1,-\sqrt{3},\frac{1}{2})$.
∴cos<$\overrightarrow{m},\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}=\frac{7\sqrt{85}}{85}$,
∴二面角M-AB-F的余弦值为$\frac{7\sqrt{85}}{85}$.
点评 本题考查线面平行的判定,考查了空间想象能力和思维能力,训练了利用空间向量求二面角的平面角,是中档题.

| A. | 向右平移$\frac{5π}{6}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{5π}{6}$个单位 | D. | 向左平移$\frac{π}{3}$个单位 |
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
| A. | 2 | B. | 3 | C. | -2 | D. | -3 |
| A. | -$\frac{4}{3}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | -$\frac{3}{5}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
