题目内容
19. 如图,若P为平行四边形ABCD所在平面外一点,点H为PC上的点,且$\frac{PH}{HC}$=$\frac{1}{2}$,点G在AH上,且$\frac{AG}{AH}$=m,若G,B,P,D四点共面,求m的值.
如图,若P为平行四边形ABCD所在平面外一点,点H为PC上的点,且$\frac{PH}{HC}$=$\frac{1}{2}$,点G在AH上,且$\frac{AG}{AH}$=m,若G,B,P,D四点共面,求m的值.
分析 若G,B,P,D四点共面,则G即为AH与平面PBD的交点,连接AC,BD交于点O,连接PO,则G即为PO与AH的交点,取HC的中点E,连接OE,结合三角形的中位线定理,可得答案.
解答 解:如下图所示: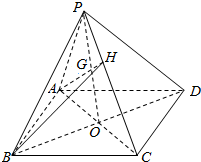
若G,B,P,D四点共面,
则G即为AH与平面PBD的交点,
连接AC,BD交于点O,连接PO,
则G即为PO与AH的交点,如下图所示: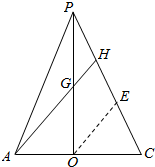
在截面PAC中,O为AC的中点,H为PC的三等分点,取HC的中点E,连接OE,
则OE=$\frac{1}{2}$AH=2GH,
故GH=$\frac{1}{4}$AH,
即AG=$\frac{3}{4}$AH,
故m=$\frac{3}{4}$.
点评 本题考查的知识点是四点共面问题,将空间问题转化为平面问题,是解答的关键.

练习册系列答案
相关题目
14.过双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F作倾斜角为45°的直线l与双曲线右支交于A、B两点,当a≤|AB|≤4a时,双曲线C的离心率的取值范围为( )
| A. | [$\frac{\sqrt{30}}{5}$,$\frac{\sqrt{6}}{2}$] | B. | (1,$\frac{\sqrt{6}}{2}$] | C. | (1,$\frac{\sqrt{30}}{5}$] | D. | [$\sqrt{2}$,+∞) |
8.在平行六面体ABCD-A′B′C′D′中,模与向量$\overrightarrow{A′B′}$的模相等的向量(不含$\overrightarrow{A′B′}$)有( )
| A. | 3个 | B. | 5个 | C. | 6个 | D. | 7个 |
13.点A(a,1)在椭圆$\frac{x^2}{4}$+$\frac{y^2}{2}$=1的内部,则a的取值范围是( )
| A. | $(-\sqrt{2},\sqrt{2})$ | B. | $(-∞,-\sqrt{2})∪(\sqrt{2},+∞)$ | C. | (-2,2) | D. | (-1,1) |
 如图,过曲线C:y=x3(x≥0)上点A1(2,8)作C的切线交x轴于点B1,过点B1作x轴的垂线交曲线C与点A2,过点A2作C的切线交x轴于点B2,再过点B2作x轴的垂线交曲线C与点A3,过点A3作C的切线交x轴于点B3,…、以此类推,得到一系列点:A1,B1,A2,B2,A3,B3,…记点An的横坐标为an.
如图,过曲线C:y=x3(x≥0)上点A1(2,8)作C的切线交x轴于点B1,过点B1作x轴的垂线交曲线C与点A2,过点A2作C的切线交x轴于点B2,再过点B2作x轴的垂线交曲线C与点A3,过点A3作C的切线交x轴于点B3,…、以此类推,得到一系列点:A1,B1,A2,B2,A3,B3,…记点An的横坐标为an.