题目内容
4．2$\sqrt{1-sin8}$-$\sqrt{2+2cos8}$=4cos4-2sin4．分析 由于2$\sqrt{1-sin8}$=2$\sqrt{（sin4-cos4）^{2}}$=2|sin4-cos4|=2cos4-2sin4，$\sqrt{2+2cos8}$=$\sqrt{4co{s}^{2}4}$=-2cos4，代入即可求得答案．
解答 解：∵π＜$\frac{5π}{4}$＜4，∴sin4＜cos4＜0，
∴2$\sqrt{1-sin8}$=2$\sqrt{（sin4-cos4）^{2}}$=2|sin4-cos4|=2cos4-2sin4，
又$\sqrt{2+2cos8}$=$\sqrt{4co{s}^{2}4}$=-2cos4，
∴2$\sqrt{1-sin8}$-$\sqrt{2+2cos8}$=2cos4-2sin4+2cos4=4cos4-2sin4．
故答案为：4cos4-2sin4．
点评 本题考查二倍角的余弦与正弦及同角三角函数间的基本关系，关键在于熟练应用二倍角公式进行转化与运算，易错点在于2$\sqrt{1-sin8}$=2cos4-2sin4的正确转化，属于中档题．
练习册系列答案
相关题目
如图，靠山有一个水库，某人先从水坝的底部A测得水坝对面的山顶P的仰角为40°，再沿坝面向上走80米到水坝的顶部B测得∠ABP=56°，若坝面与水平面所成的锐角为30°，则山高为176米；（结果四舍五入取整）
如图，若P为平行四边形ABCD所在平面外一点，点H为PC上的点，且$\frac{PH}{HC}$=$\frac{1}{2}$，点G在AH上，且$\frac{AG}{AH}$=m，若G，B，P，D四点共面，求m的值．
9．函数f（x）=x2+x-lnx的零点的个数是（ ）
| A． | 0个 | B． | 1个 | C． | 2个 | D． | 3个 |
13．桌面上放着3个半径为1的球，两两相切，在它们上方的空间里放入一个球使其顶点（最高处）恰好和3个球的顶点在同一个平面上，该球的半径为（ ）
| A． | $\frac{\sqrt{2}-1}{2}$ | B． | $\frac{\sqrt{3}-1}{3}$ | C． | $\frac{1}{3}$ | D． | $\frac{\sqrt{3}-1}{2}$ |
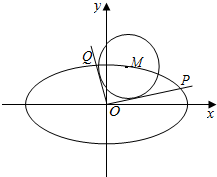如图，已知M（x0，y0）是椭圆C：$\frac{x^2}{6}+\frac{y^2}{3}=1$上的任一点，从原点O向圆M：${（{x-{x_0}}）^2}+{（{y-{y_0}}）^2}=2$作两条切线，分别交椭圆于点P、Q．