题目内容
15．已知$\overrightarrow{a}$=（4，2），$\overrightarrow{b}$=（6，y），若$\overrightarrow{a}$⊥$\overrightarrow{b}$，则y等于（ ）| A． | 3 | B． | -12 | C． | -3 | D． | 12 |
分析 运用向量垂直的条件：数量积为0，结合数量积的坐标表示，解方程即可得到所求值．
解答 解：$\overrightarrow{a}$=（4，2），$\overrightarrow{b}$=（6，y），
若$\overrightarrow{a}$⊥$\overrightarrow{b}$，
则$\overrightarrow{a}$•$\overrightarrow{b}$=4×6+2y=0，
解得y=-12．
故选：B．
点评 本题考查向量的垂直的条件：数量积为0，考查向量数量积的坐标表示，以及运算能力，属于基础题．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
5．已知复数$z=\frac{5a}{2+i}+\frac{1+i}{1-i}，a∈R$，若复数z对应的点在复平面内位于第四象限，则实数a的取值范围是（ ）
| A． | a＞1 | B． | a＜0 | C． | 0＜a＜1 | D． | a＜1 |
3．国家标准规定：轻型汽车的氮氧化物排放量不得超过80mg/km．根据这个标准，检测单位从某出租车公司运营的A、B两种型号的出租车中分别抽取5辆，对其氮氧化物的排放量进行检测，检测结果记录如下（单位：mg/km）
（Ⅰ）从被检测的5辆A型号的出租车和5辆B型号的出租车中分别抽取2辆，求抽取的这4辆车的氮氧化物排放量均不超过80mg/km的概率；
（Ⅱ）从被检测的5辆B种型号的出租车中任取2辆，记“氮氧化物排放量超过80mg/km”的车辆数为ξ，求ξ的分布列．
| A | 85 | 80 | 85 | 60 | 90 |
| B | 70 | 90 | 95 | 70 | 75 |
（Ⅱ）从被检测的5辆B种型号的出租车中任取2辆，记“氮氧化物排放量超过80mg/km”的车辆数为ξ，求ξ的分布列．
20．函数g（x）=2x+5x的零点所在的一个区间是 （ ）
| A． | （0，1） | B． | （1，2） | C． | （-1，0） | D． | （-2，-1） |
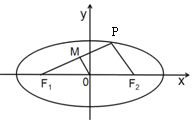已知P为椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上任意一点，F1，F2为左、右焦点，M为PF1中点．如图所示：若|OM|+$\frac{1}{2}$|PF1|=2，离心率e=$\frac{\sqrt{3}}{2}$．