题目内容
直线2x+y-1=0绕原点逆时针旋转45°后所得的直线方程为 .
考点:两直线的夹角与到角问题
专题:计算题,直线与圆
分析:旋转矩阵
=
.直线2x+y-1=0上任意一点(x0,y0)旋转变换后为(x′0,y′0),确定坐标之间的关系,即可求出直线方程.
|
| ||
| 2 |
|
解答:
解:旋转矩阵
=
.直线2x+y-1=0上任意一点(x0,y0)旋转变换后为(x′0,y′0),得
=
,
∴
,
∴直线2x+y-1=0绕原点逆时针旋转45°后所得的直线方程是x+3y=
.
故答案为:x+3y=
.
|
| ||
| 2 |
|
| ||
| 2 |
|
|
|
∴
|
∴直线2x+y-1=0绕原点逆时针旋转45°后所得的直线方程是x+3y=
| 2 |
故答案为:x+3y=
| 2 |
点评:本题考查直线方程,考查旋转矩阵,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
双曲线
-
=1的焦点到渐进线的距离等于( )
| x2 |
| 4 |
| y2 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
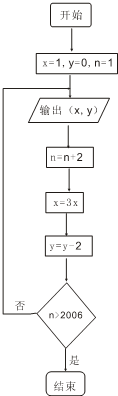 已知某算法的流程图如图示,若将输出的(x,y)依次记为(x1,y1),(x2,y2),…,(xn,yn),…
已知某算法的流程图如图示,若将输出的(x,y)依次记为(x1,y1),(x2,y2),…,(xn,yn),…