题目内容
某公司今年年初用36万元引进一种新的设备，投入设备后每年收益为21万元．同时，公司每年需要付出设备的维修和工人工资等费用，第一年各种费用2万元，第二年各种费用4万元，以后每年各种费用都增加2万元．
（1）引进这种设备后，第几年后该公司开始获利；
（2）这种设备使用多少年，该公司的年平均获利最大？
（1）引进这种设备后，第几年后该公司开始获利；
（2）这种设备使用多少年，该公司的年平均获利最大？
考点：函数模型的选择与应用
专题：应用题,函数的性质及应用
分析：（1）由题意知，每年的费用是以2为首项，2为公差的等差数列，设纯收益与使用年数n的关系为f（n），f（n）=21n-[2n+
×2]-36=20n-n2-36，由此能够求出引进这种设备后，第2年末的收益与支出恰好相等，故从第3年起该公司开始获利．
（2）年平均收益为
=20-（n+
）≤20-2
=8．由此能够求出这种设备使用6年，该公司的年平均收益最大．
| n(n-1) |
| 2 |
（2）年平均收益为
| f(n) |
| n |
| 36 |
| n |
n•
|
解答：
解：（1）由题意知，每年的费用是以2为首项，2为公差的等差数列，
设纯收益与使用年数n的关系为f（n），
则f（n）=21n-[2n+
×2]-36=20n-n2-36．…（4分）
由f（n）＞0，得n2-20n+36＜0，
解得：2＜n＜18，
∵n∈N，
∴第2年末的收益与支出恰好相等，故从第3年起该公司开始获利．…（6分）
（2）年平均收益为：
=20-（n+
）≤20-2
=8．…（10分）
当且仅当n=
，即n=6时，
取得最大值．
即这种设备使用6年，该公司的年平均收益最大．…（12分）
设纯收益与使用年数n的关系为f（n），
则f（n）=21n-[2n+
| n(n-1) |
| 2 |
由f（n）＞0，得n2-20n+36＜0，
解得：2＜n＜18，
∵n∈N，
∴第2年末的收益与支出恰好相等，故从第3年起该公司开始获利．…（6分）
（2）年平均收益为：
| f(n) |
| n |
| 36 |
| n |
n•
|
当且仅当n=
| 36 |
| n |
| f(n) |
| n |
即这种设备使用6年，该公司的年平均收益最大．…（12分）
点评：本题考查数列在生产实际中的综合应用，考查运算求解能力，推理论证能力；考查函数与方程思想，化归与转化思想．综合性强，难度大，是高考的重点．解题时要认真审题，仔细解答，注意均值定理的灵活运用．
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
相关题目
有下列调查方式：
①学校为了解高一学生的数学学习情况，从每班抽2人进行座谈；
②一次数学竞赛中，某班有15人在100分以上，35人在90～100分，10人低于90分．现在从中抽取12人座谈了解情况；
③运动会中工作人员为参加400m比赛的6名同学公平安排跑道．
就这三个调查方式，最合适的抽样方法依次为（ ）
①学校为了解高一学生的数学学习情况，从每班抽2人进行座谈；
②一次数学竞赛中，某班有15人在100分以上，35人在90～100分，10人低于90分．现在从中抽取12人座谈了解情况；
③运动会中工作人员为参加400m比赛的6名同学公平安排跑道．
就这三个调查方式，最合适的抽样方法依次为（ ）
| A、分层抽样，系统抽样，简单随机抽样 |
| B、系统抽样，系统抽样，简单随机抽样 |
| C、分层抽样，简单随机抽样，简单随机抽样 |
| D、系统抽样，分层抽样，简单随机抽样 |
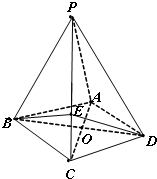如图，四棱锥P-ABCD中，底面ABCD为菱形，PA⊥底面ABCD．PA=AB=2，∠BAD=120°，E是PC上的一点，且BE与平面PAB所成角的正弦值为