题目内容
2.已知四棱锥P-ABCD中,底面ABCD是正方形,边长为4,PA=PD=$\sqrt{13}$,侧面PAD⊥底面ABCD,在四棱锥内放一个球,要使它的体积最大,则球的半径为( )| A. | 3 | B. | 2 | C. | 1 | D. | $\frac{\sqrt{2}}{2}$ |
分析 作出棱锥直观图,取AD,BC中点E,F,则棱锥内切球的半径为△PEF的内切圆的半径.
解答 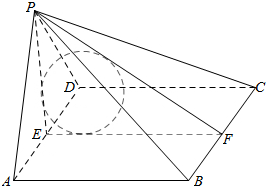 解:取AD中点E,连结PE,∵PA=PD,∴PE⊥AD,∴PE=$\sqrt{P{A}^{2}-A{E}^{2}}$=3.
解:取AD中点E,连结PE,∵PA=PD,∴PE⊥AD,∴PE=$\sqrt{P{A}^{2}-A{E}^{2}}$=3.
∵侧面PAD⊥底面ABCD,侧面PAD∩底面ABCD=AD,PE?平面PAD,PE⊥AD,
∴PE⊥平面ABCD.
取BC中点F,连结PF,EF,则PF⊥BC,EF=AB=4,∴PF=$\sqrt{P{B}^{2}-B{F}^{2}}$=5.
∴Rt△PEF的内切圆的半径即为四棱锥内切球的半径,
设Rt△PEF的内切圆的半径为r,由切线长定理得3-r+4-r=5,解得r=1.
故选C.
点评 本题主要考查棱锥的性质以及内切球的相关知识点,发现棱锥的内切球与△PEF的内切圆的关系是关键.

练习册系列答案
相关题目
13.下列函数中在(-1,1)上是减函数的是( )
| A. | y=$\frac{1}{2}$x2 | B. | y=lnx | C. | y=$\frac{2}{x}$ | D. | y=-$\frac{1}{3}$x3-2x |
10.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点为F1,F2,点P满足|PF1|+|PF2|>2a,则( )
| A. | 点P在椭圆C外 | B. | 点P在椭圆C内 | ||
| C. | 点P在椭圆C上 | D. | 点P与椭圆C的位置关系不能确定 |
11.不等式$\frac{x+1}{x-1}>2$成立的一个充分不必要条件是( )
| A. | 1<x<2 | B. | 1<x<3 | C. | 0<x<3 | D. | 1<x<4 |
