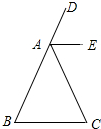题目内容
11.不等式$\frac{x+1}{x-1}>2$成立的一个充分不必要条件是( )| A. | 1<x<2 | B. | 1<x<3 | C. | 0<x<3 | D. | 1<x<4 |
分析 不等式$\frac{x+1}{x-1}>2$化为:(x-1)(x-3)<0,解出即可判断出结论.
解答 解:不等式$\frac{x+1}{x-1}>2$化为:$\frac{2(x-1)-(x+1)}{x-1}$<0,即$\frac{x-3}{x-1}$<0,
∴(x-1)(x-3)<0,解得1<x<3,
∴不等式$\frac{x+1}{x-1}>2$成立的一个充分不必要条件是1<x<2.
故选:A.
点评 本题考查了简易逻辑的判定方法、一元二次不等式与分式不等式的解法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.已知四棱锥P-ABCD中,底面ABCD是正方形,边长为4,PA=PD=$\sqrt{13}$,侧面PAD⊥底面ABCD,在四棱锥内放一个球,要使它的体积最大,则球的半径为( )
| A. | 3 | B. | 2 | C. | 1 | D. | $\frac{\sqrt{2}}{2}$ |
19.某几何体的三视图如图所示,当a+b取最大值时,该几何体体积为( )
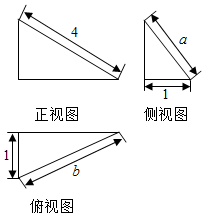

| A. | $\frac{4}{3}$ | B. | $\frac{8}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{16}{9}$ |
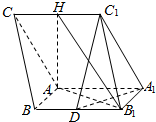 如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥侧面ABB1A1,AC=AA1=$\sqrt{2}$AB,∠AA1C1=60°.AB⊥AA1,H为棱CC1的中点,D为BB1的中点.
如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥侧面ABB1A1,AC=AA1=$\sqrt{2}$AB,∠AA1C1=60°.AB⊥AA1,H为棱CC1的中点,D为BB1的中点.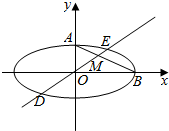 如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,点A,B分别为椭圆C的上顶点、右顶点,过坐标原点胡直线交椭圆C于D,E两点,交AB于M点,其中点E在第一象限,设直线DE的斜率为k.
如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,点A,B分别为椭圆C的上顶点、右顶点,过坐标原点胡直线交椭圆C于D,E两点,交AB于M点,其中点E在第一象限,设直线DE的斜率为k.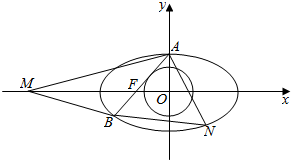 如图,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和圆C2:x2+y2=$\frac{{b}^{2}}{2}$,椭圆C1短轴的上端点为A,左焦点为F,直线AF与圆C2相切,椭圆C1左焦点到左准线的距离为1.
如图,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和圆C2:x2+y2=$\frac{{b}^{2}}{2}$,椭圆C1短轴的上端点为A,左焦点为F,直线AF与圆C2相切,椭圆C1左焦点到左准线的距离为1.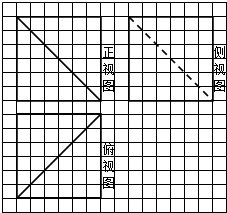 如图,网格纸上小正方形的边长为1,粗线画出的是一正方体被截去一部分后所得几何体的三视图,则被截去部分的几何体的表面积为54+18$\sqrt{3}$.
如图,网格纸上小正方形的边长为1,粗线画出的是一正方体被截去一部分后所得几何体的三视图,则被截去部分的几何体的表面积为54+18$\sqrt{3}$.