题目内容
将2n按如表的规律填在5列的数表中,设22014排在数表的第n行,第m列,则m+n= .
| 21 | 22 | 23 | 24 | |
| 28 | 27 | 26 | 25 | |
| 29 | 210 | 211 | 212 | |
| 216 | 215 | 214 | 213 | |
| … | … | … | … | … |
考点:归纳推理
专题:规律型
分析:由已知表格中,数字的填写方式,我们易发现每8个数字占两行,并可以进一步分析出数字填写的具体行和列的变化周期性规律,将2014除以周期后,代入填写规则,即可得到答案.
解答:
解:分析表中数据,发现正整数1,2,3,4,5,6,…
每8个数分为一组,填写在连续的两行中,
第一行的第2,3,4,5列各填写第一个数,
第二行的第4,3,2,1列各填写第二个数,
∵2014÷8=251…6,
故该组数字前共有251组,已经占用了502行,
22014为第252组的第6个数,
出现在该组的第二行的第3列,
故22014出现在第504行,第3列,即m=3,n=504,则m+n=507,
故答案为:507
每8个数分为一组,填写在连续的两行中,
第一行的第2,3,4,5列各填写第一个数,
第二行的第4,3,2,1列各填写第二个数,
∵2014÷8=251…6,
故该组数字前共有251组,已经占用了502行,
22014为第252组的第6个数,
出现在该组的第二行的第3列,
故22014出现在第504行,第3列,即m=3,n=504,则m+n=507,
故答案为:507
点评:本题考查的知识点是归纳推理,其中根据已知表格中填写的数字,找出数字填写的周期性规律是解答醒的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
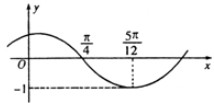 f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|<
f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|<| π |
| 2 |
A、向右平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向左平移
|
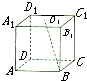 如图,正方体A1B1C1D1-ABCD中,O1是上底面A1B1C1D1的中心,若正方体的棱长为2,则O1B与CD所成角的余弦值为( )
如图,正方体A1B1C1D1-ABCD中,O1是上底面A1B1C1D1的中心,若正方体的棱长为2,则O1B与CD所成角的余弦值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
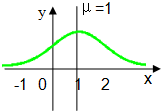 在对我市高中学生某项身体素质的测试中,测试结果ξ服从正态分布N(1,σ2)(σ>0)(如图),若ξ在(0,2)内取值的概率为0.8,则ξ在(0,1)内取值的概率为
在对我市高中学生某项身体素质的测试中,测试结果ξ服从正态分布N(1,σ2)(σ>0)(如图),若ξ在(0,2)内取值的概率为0.8,则ξ在(0,1)内取值的概率为