题目内容
已知A,B,C,D,E和F这6个人都有互联网账户,他们中的一些人(但并非所有的人)彼此之间是网友,并且他们都没有以上名单之外的网友.若他们每个人都有一样数量的朋友,则以上情况发生的可能性有 种.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:以A,B,C,D,E和F为顶点建立一个六边形,若两个人是网友,则连一条线段,然后根据题意分类讨论,综合讨论结果可得答案.
解答:
 解:如下图所示:
解:如下图所示:
若两个人是网友,则连一条线段,
∵并非所有人是网友,可知每个人最多有4个朋友,
①若每个人均有1个朋友,则表示图中只有3条没有公共顶点的线段,
共有
•
•
÷
=15种选法,
②若每个人均有2个朋友,则每一个顶点均发出2条边,
显然可以构成一个长度为6的圈或者两个长度为3的圈,
则有
+
=70种选法;
③若每个人均有3个朋友,则每一个顶点均发出3条边,
即每一个顶点均不和某2个顶点相连,此时结果同②,
④若每个人均有4个朋友,则每一个顶点均发出4条边,
即每一个顶点均不和某1个顶点相连,此时结果同①,
于是有15+70+70+15=170种可能性.
故答案为:170
 解:如下图所示:
解:如下图所示:若两个人是网友,则连一条线段,
∵并非所有人是网友,可知每个人最多有4个朋友,
①若每个人均有1个朋友,则表示图中只有3条没有公共顶点的线段,
共有
| C | 2 6 |
| C | 2 4 |
| C | 2 2 |
| A | 3 3 |
②若每个人均有2个朋友,则每一个顶点均发出2条边,
显然可以构成一个长度为6的圈或者两个长度为3的圈,
则有
| ||
| 2 |
| ||
| 2 |
③若每个人均有3个朋友,则每一个顶点均发出3条边,
即每一个顶点均不和某2个顶点相连,此时结果同②,
④若每个人均有4个朋友,则每一个顶点均发出4条边,
即每一个顶点均不和某1个顶点相连,此时结果同①,
于是有15+70+70+15=170种可能性.
故答案为:170
点评:本题考查的知识点是排列组合,其中合理的确定分类标准后,进行分类讨论,是解答的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在高台跳水运动中,已知运动员相对于水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系h(t)=-4.9t2+6.5t+10,则运动员在t=1s时的瞬间速度为( )
| A、3.3m/s |
| B、-3.3m/s |
| C、11.6m/s |
| D、-11.6m/s |
下列说法正确的是( )
| A、命题“若x2-5x+6=0,则x=2”的逆命题是“若x≠2,则x2-5x+6≠0” |
| B、命题“若x=2,则x2-5x+6=0”的否命题是“若x=2,则x2-5x+6≠0” |
| C、已知a,b∈R,则“a>b”是“|a|>|b|”的充要条件 |
| D、已知a,b∈R,则“ab≠0”是“a≠0”的充分条件 |
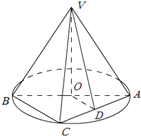 如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,D是AC的中点,已知AB=2,VA=VB=VC=2.
如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,D是AC的中点,已知AB=2,VA=VB=VC=2.