题目内容
 如图,在△AOB中,已知∠AOB=60°,OA=2,OB=5,在线段OB上任取一点C,求△AOC为锐角三角形的概率为( )
如图,在△AOB中,已知∠AOB=60°,OA=2,OB=5,在线段OB上任取一点C,求△AOC为锐角三角形的概率为( )| A、0.6 | B、0.4 |
| C、0.2 | D、0.1 |
考点:几何概型
专题:概率与统计
分析:由已知条件利用勾股定理求出△AOC三个角都是锐角时1<OC<4,由此能求出其概率.
解答:
解:△AOC为锐角三角形时,∠ACO为锐角,且∠OAB是锐角.
当∠ACO=90°时,有勾股定理求得OC=1,
∠OAC=90°时,由直角三角形中的边角关系,解得OC=4,BC=1
综上,△AOC三个角都是锐角时1<OC<4,
其概率为:
p=
=
=0.6.
故选:A.

当∠ACO=90°时,有勾股定理求得OC=1,
∠OAC=90°时,由直角三角形中的边角关系,解得OC=4,BC=1
综上,△AOC三个角都是锐角时1<OC<4,
其概率为:
p=
| 4-1 |
| 5 |
| 3 |
| 5 |
故选:A.
点评:本题考果概率的求法,是中档题,解题时要认真审题,注意勾股定理的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
(x-
)9展开式中x3的系数是( )
| 1 |
| x |
| A、48 | B、-48 |
| C、84 | D、-84 |
数列{an}满足a0=
,an+1=[an]+
,([an]与{an}分别表示an的整数部分与分数部分),则a2014=( )
| 3 |
| 1 |
| {an} |
A、3020+
| ||||
B、3020+
| ||||
C、
| ||||
D、3018+
|
由数字0,1,2,3,4可组成无重复数字的两位数的个数是( )
| A、25 | B、20 | C、16 | D、12 |
用10元、5元和1元来支付20元钱的书款,不同的支付方法有( )
| A、3 | B、5 | C、9 | D、12 |
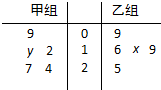 如图茎叶图记录了甲乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的中位数为17,乙组数据的平均数为17.4,则x,y的值分别为( )
如图茎叶图记录了甲乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的中位数为17,乙组数据的平均数为17.4,则x,y的值分别为( )| A、7,8 | B、5,7 |
| C、8,5 | D、8,7 |
在等差数列{an}中,a1+a2+a3=3,a28+a29+a30=165,则此数列前30项和等于( )
| A、810 | B、840 |
| C、870 | D、900 |