题目内容
在等差数列{an}中，a1+a2+a3=3，a28+a29+a30=165，则此数列前30项和等于（ ）
| A、810 | B、840 |
| C、870 | D、900 |
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：在等差数列{an}中，由a1+a2+a3=3，a28+a29+a30=165，知a1+a30=56，再由S30=15（a1+a30），能求出此数列前30项和．
解答：
解：在等差数列{an}中，
∵a1+a2+a3=3，a28+a29+a30=165，
∴3（a1+a30）=168，
∴a1+a30=56，
∴此数列前30项和为S30=15（a1+a30）=15×56=840．
故选：B．
∵a1+a2+a3=3，a28+a29+a30=165，
∴3（a1+a30）=168，
∴a1+a30=56，
∴此数列前30项和为S30=15（a1+a30）=15×56=840．
故选：B．
点评：本题考查等差数列的前n项公式和通项公式，考查等差数列的性质，是中档题．
练习册系列答案
优化作业上海科技文献出版社系列答案
相关题目
如图，在△AOB中，已知∠AOB=60°，OA=2，OB=5，在线段OB上任取一点C，求△AOC为锐角三角形的概率为（ ）| A、0.6 | B、0.4 |
| C、0.2 | D、0.1 |
2011是等差数列：1，4，7，10…的第（ ）项．
| A、669 | B、670 |
| C、671 | D、672 |
已知双曲线
-
=1（a＞0，b＞0）与抛物线y2=2px（p＞0）有一个共同的焦点F，点M是双曲线与抛物线的一个交点，若|MF|=
p，则此双曲线的离心率等于（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
| 4 |
| A、2 | ||
| B、3 | ||
C、
| ||
D、
|
△ABC的内角A、B、C所对的边分别为a，b，c．若B=2A，a=1，b=
，则这样的三角形有（ ）
| 2 |
| A、只有一个 | B、有两个 |
| C、不存在 | D、无数个 |
已知某随机变量X的分布如下（p，q∈R）
且X的数学期望E（X）=
，那么X的方差D（X）等于（ ）
| X | 1 | -1 |
| P | p | q |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
| D、1 |
复数i3的值是（ ）
| A、-i | B、1 | C、-1 | D、i |
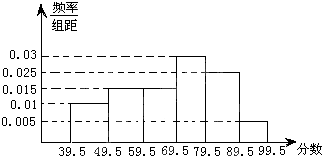如图，从参加环保知识竞赛的学生中抽出60名，将其成绩（均为整数）整理后画出的频率分布直方图如图所示，观察图形，回答下列问题：