题目内容
6.△ABC中,sinA:sinB:sinC=2:4;5,判断三角形的形状.分析 由sinA:sinB:sinC=2:4;5,利用正弦定理可得:a:b:c=2:4;5,不妨取a=2,b=4,c=5,利用余弦定理求出cosC,即可得出.
解答 解:∵sinA:sinB:sinC=2:4;5,
由正弦定理可得:a:b:c=2:4;5,
不妨取a=2,b=4,c=5,
由余弦定理可得:cosC=$\frac{{2}^{2}+{4}^{2}-{5}^{2}}{2×2×4}$<0,
∵C∈(0,π),∴C为钝角,
∴△ABC为钝角三角形.
点评 本题考查了正弦定理余弦定理的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
17.命题p:若ab=0,则a=0;命题q:3≥3,则( )
| A. | “p或q”为假 | B. | “p且q”为真 | C. | p真q假 | D. | p假q真 |
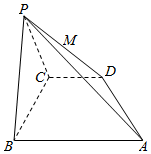 在四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠ABC=90°,AB=PB=PC=BC=2CD,平面PBC⊥平面ABCD,M为PD的中点,过A,B,M的平面记为α.
在四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠ABC=90°,AB=PB=PC=BC=2CD,平面PBC⊥平面ABCD,M为PD的中点,过A,B,M的平面记为α.