题目内容
18.边长为$4\sqrt{2}$的正方形ABCD的四个顶点在半径为5的球O的表面上,则四棱锥O-ABCD的体积是32.分析 求出四棱锥O-ABCD的高,然后求解几何体的体积.
解答 解:边长为$4\sqrt{2}$的正方形ABCD的四个顶点在半径为5的球O的表面上,可知四棱锥O-ABCD的对面边长为4$\sqrt{2}$,侧棱长为5,棱锥的高为:$\sqrt{{5}^{2}-{4}^{2}}$=3.
四棱锥O-ABCD的体积是:$\frac{1}{3}×4\sqrt{2}×4\sqrt{2}×3$=32.
故答案为:32.
点评 本题考查棱锥的体积的求法,求出棱锥的高是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.一个四棱锥的底面为菱形,其三视图如图所示,则这个四棱锥的体积是( )
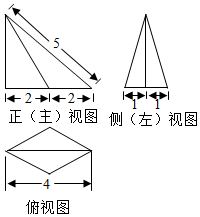

| A. | 2 | B. | 4 | C. | 8 | D. | 12 |
10.已知i是虚数单位,复数z=(a+i)(1-i),若z的实部与虚部相等,则实数a=( )
| A. | 1 | B. | 0 | C. | -1 | D. | -2 |
7.按顺序输入x,y,z的值,运行如图的程序后,输出的结果为8,则输入的x,y,z的值可能是( )
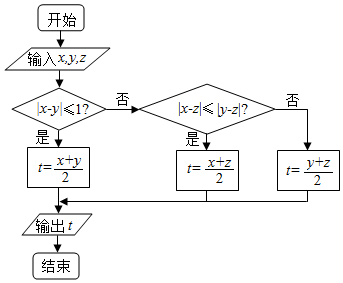

| A. | x=6,y=8,z=9 | B. | x=8,y=7,z=9 | C. | x=8,y=6,z=10 | D. | x=8,y=6,z=8 |
8.已知函数f(x)=x3-x2-x+a的图象与x轴只有一个交点,则实数a的取值范围是( )
| A. | (-∞,-1)∪(-$\frac{1}{9}$,+∞) | B. | (-$\frac{5}{27}$,1) | C. | (-∞,1) | D. | (-∞,-$\frac{5}{27}$)∪(1,+∞) |
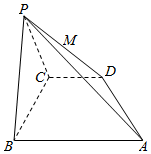 在四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠ABC=90°,AB=PB=PC=BC=2CD,平面PBC⊥平面ABCD,M为PD的中点,过A,B,M的平面记为α.
在四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠ABC=90°,AB=PB=PC=BC=2CD,平面PBC⊥平面ABCD,M为PD的中点,过A,B,M的平面记为α.