题目内容
已知已知M={a|f(x)=2sinax 在[-
,
]上是增函数},N={b|方程3-|x-1|-b+1=0有实数解},设D=M∩N,函数f(x)=
是定义在R上的奇函数,则下列命题中正确的是 (填出所有正确命题的序号)
①m=(-∞,
];
②N=(0,2);
③D=(1,
];
④n=0,m∈R;
⑤如果f(x)在D上没有最小值,那么m的取值范围是(
,+∞).
| π |
| 3 |
| π |
| 4 |
| x+n |
| x2+m |
①m=(-∞,
| 3 |
| 2 |
②N=(0,2);
③D=(1,
| 3 |
| 2 |
④n=0,m∈R;
⑤如果f(x)在D上没有最小值,那么m的取值范围是(
| 3 |
| 2 |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:本题①先研究函数f(x)=2sinax的周期和0附近单调区间[-
,
],然后比较[-
,
]与[-
,
],求出m的取值范围,得到选项①不正确;
再将3-|x-1|-b+1=0,变形为b=3-|x-1|+1,研究函数值域,得到1<b≤2,得到选项②不正确;
求M、N的交集,得到D=M∩N=(1,
],选项③正确;
由函数f(x)的定义为R,得到x2+m≠0恒成立,从而有m>0.得到故选项④不成立;
再变形研究函数f(x)取值情况,得到x+
无最大值,记g(x)=x+
,
则g(1)>g(
),得到m>
.故知选项⑤正确.
| π |
| 2|a| |
| π |
| 2|a| |
| π |
| 3 |
| π |
| 4 |
| π |
| 2|a| |
| π |
| 2|a| |
再将3-|x-1|-b+1=0,变形为b=3-|x-1|+1,研究函数值域,得到1<b≤2,得到选项②不正确;
求M、N的交集,得到D=M∩N=(1,
| 3 |
| 2 |
由函数f(x)的定义为R,得到x2+m≠0恒成立,从而有m>0.得到故选项④不成立;
再变形研究函数f(x)取值情况,得到x+
| m |
| x |
| m |
| x |
则g(1)>g(
| 3 |
| 2 |
| 3 |
| 2 |
解答:
解:选项①,
∵函数f(x)=2sinax的周期为
,(a≠0)
∴函数f(x)=2sinax在区间[-
,
]上单调递增,
∵f(x)=2sinax 在[-
,
]上是增函数,
∴-
≤-
,
≤
,
∴|a|≤
.
∴a∈[-
,0)∪(0,
].
∵M={a|f(x)=2sinax 在[-
,
]上是增函数},
∴M=[-
,0)∪(0,
]∪(0,
].
故选项①不正确.
选项②,
又∵3-|x-1|-b+1=0,
∴b=3-|x-1|+1>1,
b=3-|x-1|+1≤30+1=2,
∴1<b≤2.
∵N={b|方程3-|x-1|-b+1=0有实数解},
∴N=(1,2].
故选项②不正确.
选项③,
∵M=[-
,0)∪(0,
]∪(0,
],N=(1,2],
∴D=M∩N=(1,
].
故选项③正确.
选项④,
∵函数f(x)=
是奇函数,
∴
=-
,
∴n=0,
∵函数f(x)的定义为R,
∴x2+m≠0恒成立,
∴m>0.
故选项④不成立.
∴函数f(x)=
=
,(m>0).
选项⑤,
要使f(x)在区间(1,
]上无最小值,
则要x+
无最大值,
记g(x)=x+
,
则g(1)>g(
),
∴1+m>
+
,
∴m>
.
故选项⑤正确.
故答案为:③⑤.
∵函数f(x)=2sinax的周期为
| 2π |
| |a| |
∴函数f(x)=2sinax在区间[-
| π |
| 2|a| |
| π |
| 2|a| |
∵f(x)=2sinax 在[-
| π |
| 3 |
| π |
| 4 |
∴-
| π |
| 2|a| |
| π |
| 3 |
| π |
| 4 |
| π |
| 2|a| |
∴|a|≤
| 3 |
| 2 |
∴a∈[-
| 3 |
| 2 |
| 3 |
| 2 |
∵M={a|f(x)=2sinax 在[-
| π |
| 3 |
| π |
| 4 |
∴M=[-
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
故选项①不正确.
选项②,
又∵3-|x-1|-b+1=0,
∴b=3-|x-1|+1>1,
b=3-|x-1|+1≤30+1=2,
∴1<b≤2.
∵N={b|方程3-|x-1|-b+1=0有实数解},
∴N=(1,2].
故选项②不正确.
选项③,
∵M=[-
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
∴D=M∩N=(1,
| 3 |
| 2 |
故选项③正确.
选项④,
∵函数f(x)=
| x+n |
| x2+m |
∴
| -x+n |
| (-x)2+m |
| x+n |
| x2+m |
∴n=0,
∵函数f(x)的定义为R,
∴x2+m≠0恒成立,
∴m>0.
故选项④不成立.
∴函数f(x)=
| x |
| x2+m |
| 1 | ||
x+
|
选项⑤,
要使f(x)在区间(1,
| 3 |
| 2 |
则要x+
| m |
| x |
记g(x)=x+
| m |
| x |
则g(1)>g(
| 3 |
| 2 |
∴1+m>
| 3 |
| 2 |
| 2m |
| 3 |
∴m>
| 3 |
| 2 |
故选项⑤正确.
故答案为:③⑤.
点评:本题考查了函数的奇偶性、单调性、函数的定义域、值域、图象与最值,本题有一定的综合性,难度适中,属于中档题.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
若直线与平面所成的角为0°,则该直线与平面的位置关系是( )
| A、平行 | B、相交 |
| C、直线在平面内 | D、平行或直线在平面内 |
设集合A={x|x2-4x<0},B={x|x-2>0},则A∩B=( )
| A、(0,2) |
| B、(0,4) |
| C、(4,+∞) |
| D、(2,4) |
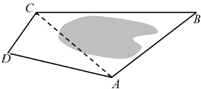 如图为了测量A,C两点间的距离,选取同一平面上B,D两点,测出四边形ABCD各边的长度(单位:km):AB=5,BC=8,CD=3,DA=5,如图所示,且A、B、C、D四点共圆,则AC的长为
如图为了测量A,C两点间的距离,选取同一平面上B,D两点,测出四边形ABCD各边的长度(单位:km):AB=5,BC=8,CD=3,DA=5,如图所示,且A、B、C、D四点共圆,则AC的长为