题目内容
设集合A={x|x2-4x＜0}，B={x|x-2＞0}，则A∩B=（ ）
| A、（0，2） |
| B、（0，4） |
| C、（4，+∞） |
| D、（2，4） |
考点：并集及其运算
专题：集合
分析：求出集合A，B，利用交集的运算即可得到结论．
解答：
解：因为A={x|x2-4x＜0}={x|0＜x＜4}，
B={x|x-2＞0]}={x|x＞2}，
所以A∩B={x|2＜x＜4}=（2，4），
故选：D．
B={x|x-2＞0]}={x|x＞2}，
所以A∩B={x|2＜x＜4}=（2，4），
故选：D．
点评：本题考查交集及其运算，求出集合A，B是解决本题的关键．
练习册系列答案
名题训练系列答案
期末集结号系列答案
相关题目
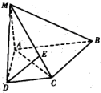如图，在四棱锥M-ABCD中，底面ABCD是直角梯形，AB∥DC，∠ABC=45°，DC-2，AB=4，MA=2，MA⊥平面ABCD．