题目内容
8.已知向量$\overrightarrow{a}$=(cosx,-$\frac{\sqrt{3}}{2}$),$\overrightarrow{b}$=(sinx,cos2x),x∈R,设函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$.(I)求f(x)的最小正周期:
(Ⅱ)若x∈(0,$\frac{π}{2}$),求函数f(x)的值域.
分析 (Ⅰ)由向量的数量积求出函数f(x)=sin(2x-$\frac{π}{3}$),由此能求出f(x)的最小正周期.
(Ⅱ)由x∈(0,$\frac{π}{2}$),知2x-$\frac{π}{3}$∈(-$\frac{π}{3}$,$\frac{2π}{3}$),由此能求出函数f(x)的值域.
解答 解:(Ⅰ)∵向量$\overrightarrow{a}$=(cosx,-$\frac{\sqrt{3}}{2}$),$\overrightarrow{b}$=(sinx,cos2x),x∈R,
∴函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$=cosxsinx-$\frac{\sqrt{3}}{2}$cos2x
=$\frac{1}{2}sin2x-\frac{\sqrt{3}}{2}cos2x$=sin(2x-$\frac{π}{3}$),
∴f(x)的最小正周期T=$\frac{2π}{2}$=π.
(Ⅱ)∵x∈(0,$\frac{π}{2}$),∴2x-$\frac{π}{3}$∈(-$\frac{π}{3}$,$\frac{2π}{3}$),
∴当2x-$\frac{π}{3}$→-$\frac{π}{3}$时,f(x)min→-$\frac{\sqrt{3}}{2}$,当2x-$\frac{π}{3}$=$\frac{π}{2}$时,f(x)max=1,
∴函数f(x)的值域为(-$\frac{\sqrt{3}}{2}$,1].
点评 本题考查三角函数的周期性的求法,考查三角函数的值域的求法,涉及到向量数量积公式、三角函数恒等式变换、三角函数图象及性质等知识点,是中档题.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
2.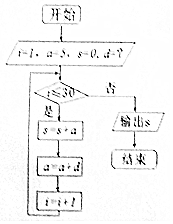 《九章算术》之后,人们学会了用数列的知识来解决问题.公元5世纪中国古代内容丰富的数学著作《张丘建算经》卷上有题为:“今有女善织,日益功疾,初日织五尺,今一月织九匹三丈.问日益几何?”.利用这种思想设计的一个程序框图如图,若输出的S值为九匹三丈(一匹=4丈,一丈=10尺),则框图中d为( )
《九章算术》之后,人们学会了用数列的知识来解决问题.公元5世纪中国古代内容丰富的数学著作《张丘建算经》卷上有题为:“今有女善织,日益功疾,初日织五尺,今一月织九匹三丈.问日益几何?”.利用这种思想设计的一个程序框图如图,若输出的S值为九匹三丈(一匹=4丈,一丈=10尺),则框图中d为( )
 《九章算术》之后,人们学会了用数列的知识来解决问题.公元5世纪中国古代内容丰富的数学著作《张丘建算经》卷上有题为:“今有女善织,日益功疾,初日织五尺,今一月织九匹三丈.问日益几何?”.利用这种思想设计的一个程序框图如图,若输出的S值为九匹三丈(一匹=4丈,一丈=10尺),则框图中d为( )
《九章算术》之后,人们学会了用数列的知识来解决问题.公元5世纪中国古代内容丰富的数学著作《张丘建算经》卷上有题为:“今有女善织,日益功疾,初日织五尺,今一月织九匹三丈.问日益几何?”.利用这种思想设计的一个程序框图如图,若输出的S值为九匹三丈(一匹=4丈,一丈=10尺),则框图中d为( )| A. | $\frac{1}{2}$尺 | B. | $\frac{8}{15}$尺 | C. | $\frac{16}{31}$尺 | D. | $\frac{16}{29}$尺 |
3.设a,b,c,d是四条不同的直线,且a,b为异面直线,命题p“c与a,b都相交,d与a,b都相交”,命题q“c,d为相交直线”,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
13.已知函数f(x)的图象在点(x0,f(x0))处的切线方程l:y=g(x),若函数f(x)满足?x∈I(其中I为函数f(x)的定义域),当x≠x0时,[f(x)-g(x)](x-x0)>0恒成立,则称x0为函数f(x)的“穿越点”.已知函数f(x)=lnx-$\frac{a}{2}$x2-$\frac{x}{2}$在(0,e]上存在一个“穿越点”,则a的取值范围为( )
| A. | [$\frac{1}{{e}^{2}}$,+∞) | B. | (-1,$\frac{1}{{e}^{2}}$] | C. | [-$\frac{1}{{e}^{2}}$,1) | D. | (-∞,-$\frac{1}{{e}^{2}}$] |
17.为了得到函数y=sin(2x-$\frac{π}{3}$)的图象,只需将函数y=sin2x的图象上所有的点( )
| A. | 向左平移$\frac{π}{6}$个单位 | B. | 向左平移$\frac{π}{3}$个单位 | ||
| C. | 向右平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{π}{3}$个单位 |
18.已知三棱锥P-ABC的四个顶点P,A,B,C都在半径为R的同一个球面上,若PA,PB,PC两两相互垂直,且PA=1,PB=2,PC=3,则R等于( )
| A. | $\frac{{\sqrt{14}}}{2}$ | B. | $\sqrt{14}$ | C. | $\frac{{\sqrt{13}}}{2}$ | D. | $\sqrt{3}$ |