题目内容
18.已知直线l:$ρsin(θ+\frac{π}{3})=\frac{{\sqrt{3}}}{2}m$,曲线C:$\left\{\begin{array}{l}x=1+\sqrt{3}cosθ\\ y=\sqrt{3}sinθ\end{array}\right.$(1)当m=3时,判断直线l与曲线C的位置关系;
(2)若曲线C上存在到直线l的距离等于$\frac{{\sqrt{3}}}{2}$的点,求实数m的范围.
分析 (1)分别化为直角坐标方程,求出圆心到直线的距离d与半径比较即可得出结论.
(2)曲线C上存在到直线l的距离等于$\frac{{\sqrt{3}}}{2}$的点,可得圆心C(1,0)到直线l的距离d=$\frac{|\sqrt{3}-m\sqrt{3}|}{2}$≤r+$\frac{\sqrt{3}}{2}$,
解出即可得出.
解答 解:(1)直线l:$ρsin(θ+\frac{π}{3})=\frac{{\sqrt{3}}}{2}m$,展开可得:$ρ(\frac{1}{2}sinθ+\frac{\sqrt{3}}{2}cosθ)$=$\frac{\sqrt{3}}{2}$m,
化为直角坐标方程:y+$\sqrt{3}$x=$\sqrt{3}$m,
m=3时,化为:y+$\sqrt{3}$x-3$\sqrt{3}$=0,
曲线C:$\left\{\begin{array}{l}x=1+\sqrt{3}cosθ\\ y=\sqrt{3}sinθ\end{array}\right.$,利用平方关系化为:(x-1)2+y2=3.
圆心C(1,0)到直线l的距离d=$\frac{|\sqrt{3}-3\sqrt{3}|}{2}$=$\sqrt{3}$=r,
因此直线l与曲线C相切.
(2)∵曲线C上存在到直线l的距离等于$\frac{{\sqrt{3}}}{2}$的点,
∴圆心C(1,0)到直线l的距离d=$\frac{|\sqrt{3}-m\sqrt{3}|}{2}$≤$\sqrt{3}$+$\frac{\sqrt{3}}{2}$,
解得-2≤m≤4.
∴实数m的范围是[-2,4].
点评 本题考查了极坐标方程回去直角坐标方程、参数方程化为普通方程、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.

 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案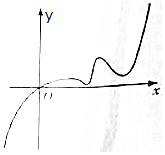 已知函数f(x)的定义域为R,且f(2)=2,又函数f(x)的导函数y=f′(x)的图象如图所示,若两个正数a、b满足f(2a+b)<2,则$\frac{b+2}{a+2}$的取值范围是( )
已知函数f(x)的定义域为R,且f(2)=2,又函数f(x)的导函数y=f′(x)的图象如图所示,若两个正数a、b满足f(2a+b)<2,则$\frac{b+2}{a+2}$的取值范围是( )| A. | ($\frac{2}{3}$,2) | B. | (-∞,$\frac{2}{3}$)∪(2,+∞) | C. | (2,+∞) | D. | (-∞,$\frac{2}{3}$) |
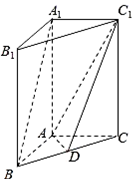 如图,在直三棱锥A1B1C1-ABC,AB⊥AC,AB=AC=2,AA1=4,点D是BC的中点.
如图,在直三棱锥A1B1C1-ABC,AB⊥AC,AB=AC=2,AA1=4,点D是BC的中点.